Черное излучение

Важнейшим примером применения статистики Бозе является электромагнитное излучение, находящееся в тепловом равновесии – так называемое черное излучение.

Черное излучение можно рассматривать как газ, состоящий из фотонов. Линейность уравнений электродинамики отражает тот факт, что фотоны не взаимодействуют друг с другом (принцип суперпозиции ), так что фотонный газ можно считать идеальным. Фотоны имеют спин равный единице, и подчиняются статистике Бозе.

Если измерение находится не в вакууме, а в материальной среде, то условие идеальности фотонного газа требует малости взаимодействия излучения с веществом. Это условие выполнимо в газах (за исключением частот близких к линиям поглощения). При большой плотности – только при очень больших температурах.

Следует иметь в виду, что наличие хотя бы небольшого количества вещества вообще необходимо для самой возможности установления теплового равновесия в излучении, так как фотоны практически не взаимодействуют между собой.

Число частиц N в фотонном газе – переменная величина, т.к. они поглощаются и излучаются атомами. Поэтому N должна сама определяться из условия равновесия. Потребовав минимальности свободной энергии газа (при заданных T,V) получим в качестве одного из необходимых условий ∂F/∂N = 0. Но поскольку (∂F/∂N) T,V = μ, отсюда следует, что μ = 0 для газа фотонов.

Распределение фотонов по различным газовым состояниям с определенными значениями импульса (и определенной поляризации) дается, следовательно, формулой (с μ = 0)

                                                 (*).

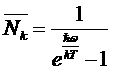Это так называемое распределение Планка. Считая объем достаточно большим, перейдем от дискретного к непрерывному распределению собственных частот излучения.

Число колебаний с компонентами волнового вектора  в интервалах d3k = dkxdkydkz равно Vd3k/(2π)3, а число колебаний с абсолютной величиной волнового вектора в интервале dk есть, соответственно 4πk3dkV/(2π)3.

Вводя частоту ω=сk и умножая на 2 (два независимых направления поляризации колебаний), получим число квантовых состояний фотонов с частотами в интервале {ω, ω+d ω}

V ω2d ω/(π2c3).

Умножив распределение (*) на эту величину, найдем число фотонов в данном интервале частот

,

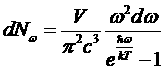 а умножив ещё на hω, получим энергию излучения, заключенную в этом участке спектра:

 .                                        (**)

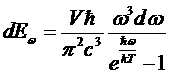Эта формула для спектрального распределения черного излучения называется формулой Планка. При hω<<kT она переходит в формулу Рэлея –Джинса

.

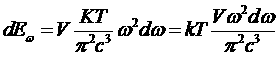Это формула не содержит постоянной Планка h. Ее смысл достаточно прост: в классической механике на каждую колебательную степень свободы должна приходиться энергия kT (закон равнораспределения).

В другом предельном случае hω>>kT

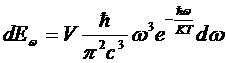
 - формула Вина.

При этом имеет место закон смещения Вина – максимум распределения при повышении температуры смещается в сторону больших частот, пропорциональных T.

Вычислим термодинамические величины черного излучения. При μ = 0 свободная энергия F совпадает с Ω (F = Ф – PV = μN +Ω)

Согласно формуле

,

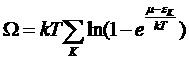где полагаем μ = 0 и переходим обычным образом 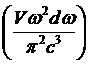 от суммирования к интегрированию, получим:

.

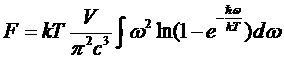Вводя безразмерную переменную интегрирования, и интегрируя по частям, получим:

.

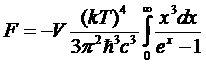Стоящий здесь интеграл равен π4/15. Таким образом:

,

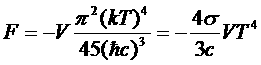где 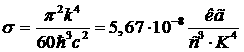- постоянная Стефана-Больцмана

Энтропия черного излучения равна

.

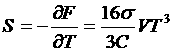Полная энергия излучения

.

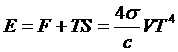Это выражение можно получить и интегрированием (**). Оно представляет собой обоснование закона Больцмана – полная энергия излучения ~T4 .

Найдем теплоемкость излучения

.

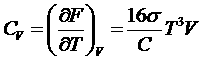Давление черного излучения:

.

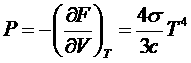Видим, что давление не зависит от V (при изотермическом сжатии давление не меняется), что является следствием переменности числа частиц. Из этого выражения можно получить

.

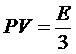Полное число фотонов в черном излучении

.

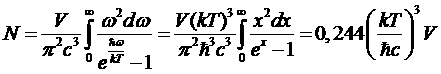Статистический вывод закона Стефана-Больцмана

Этот закон был открыт Стефаном (австрия) экспериментально в 1879 году путем измерения теплоотдачи платиновой проволоки. Теоретическое обоснование этог закона было дано учеником Стефана Больцманом в 1884 году на основе следствий теории электромагнитного поля Максвелла.

Рассмотрим излучение фотонов с поверхности абсолютно черного тела. Найдем сначала распределение вылетающих фотонов по углам.Пусть частицы вылетают из точки А (рис.). Выделим сферу радиуса R с центром в этой точке. В равновесии все направления полета фотонов равновероятны. Это означает, что вероятность для фотона попасть в какую-либо часть полусферы будет равна отношению:

,

где dS – элементарная площадка на полусфере, а в знаменателе стоит площадь полусферы.

Выделим элементарную площадку для фотонов, угол отклонения которых от вертикали находится в интервале (Θ, Θ+dΘ):

,

где dl – элемент дуги окружности.

Имея в виду, что

,

а так же то, что

,

получим:

,

.

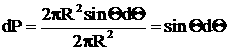Это и есть функция распределения вылетающих фотонов по углам. Легко убедиться в том, что она нормирована. Таким образом, можно сделать вывод о том, что фотоны вылетают главным образом с большими углами от вертикали.

Найдем плотность потока энергии излучения – количество энергии, излучаемой в секунду с единицы поверхности.

Выделим вблизи поверхности, площадью S малый объем высотой cdt и найдем, сколько энергии из этого объема упадет на стенку.

В этом объеме заключена энергия:

.

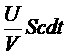Однако на стенку попадет только часть этой энергии. Во-первых, нас будут интересовать только фотоны, имеющие положительную составляющую скорости по оси x (их ровно половина). С другой стороны, на основе распределения фотонов по углам можно записать:

.

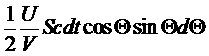Здесь cosΘ появляется в результате проецирования скорости на ось x.

Введем плотность потока энергии:

.

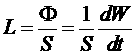Таким образом, для плотности потока энергии получим:

.

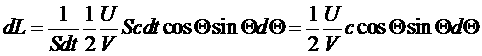Интегрируя по углам, получим:

.

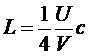Но поскольку ранее было получено, что

,

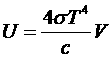то окончательно получаем Закон Стефана-Больцмана:

.