Двухатомный газ с молекулами из различных атомов. Вращение молекул

Будем рассматривать теперь идеальные газы с учетом внутренней структуры их молекул. Наиболее простой случай представляет собой двухатомный газ. Двухатомный газ можно рассматривать как таковой только при условии малости kТ по сравнению с энергией диссоциации молекул. В таблице приведены характерные температуры, соответствующие диссоциации некоторых молекул.

Наиболее важный практический случай – когда в своем нормальном электронном состоянии молекула газа не имеет ни спина, ни орбитального момента вращения относительно оси (нет тонкой структуры). Следует различать случаи молекул, составленных из разных атомов (изотопы) и молекул, составленных из одинаковых атомов. Будем считать, что атомы разные (не тождественные).

Уровень энергии двухатомной молекулы складывается в известном приближении из трех независимых частей – электронной энергии (энергии кулоновского взаимодействия ядер в их равновесном положении, отсчитываемой от суммы энергий разведенных атомов); вращательной энергии и энергии колебания ядер внутри молекулы. Эти уровни могут быть записаны в следующем виде:

.

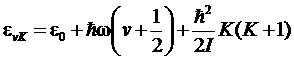При классическом вращении энергия имеет вид

,

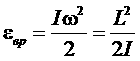но из квантовой механики следует, что L2 квантуется.

Здесь ε0-электронная энергия, – колебательный квант, v – колебательное квантовое число, К – вращательное квантовое число;
I = m’r02 – момент инерции молекулы, m’ – приведенная масса обоих атомов, r0 – равновесное состояние между атомами.

При подстановке этого выражения в статическую сумму, последняя распадается на три независимых множителя:

,

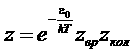где вращательная и колебательная суммы определяются как

,

,

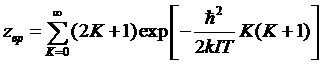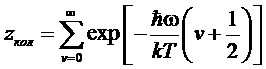причем множитель 2К+1 в zвр учитывает вырождение вращательных уровней по направлениям момента импульса L. Соответственно, свободная энергия представится как:

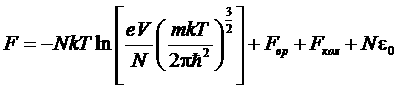
(m=m1+m2) – масса молекулы. Первый член можно назвать поступательной частью Fпос (поскольку он связан со степенями свободы поступательного движения молекул), а

, .

Поступательная теплоемкость, приходящаяся на одну молекулу, равна cпос=3/2 k. Полная теплоемкость газа записывается в виде суммы

cV= cпос+ cвр + cкол;                  cр= cпос+ cвр + cкол + k,

каждое слагаемое которой связано с тепловым возбуждением соответственно поступательного, вращательного и колебательного движений.

Вычислим вращательную свободную энергию.

Рассмотрим случай, когда температура настолько высока, что

.

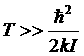 Это означает, что вращательный квант  мал по сравнению с тепловой энергией kТ. В таблице представлены величины  для некоторых двухатомных молекул.

В этом случае в сумме Zвр основную роль играют члены с большими числами К. Но при больших значениях К вращение молекулы квазиклассично. Поэтому в этом случае статистическая сумма Zврможет быть замечена соответствующим классическим интегралом по К:

.

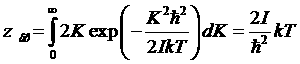Отсюда свободная энергия

.

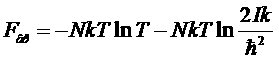Таким образом при рассматриваемых не слишком низких Т вращательная часть теплоемкости оказывается равной k (в соответствии с общим результатом классического рассмотрения по k/2 на каждую степень свободы):

, , , .

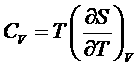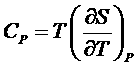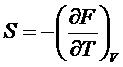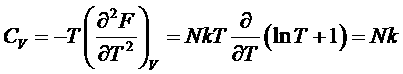Мы увидим ниже, что существует значительная область температур, в которой выполнено условие 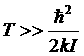 и в то же время колебательная часть свободной энергии, а значит и колебательная часть теплоемкости отсутствуют. В этой области теплоемкость двухатомного газа, приходящаяся на одну молекулу, равна

, .

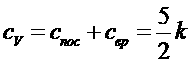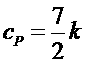Рассмотрим теперь обратный предельный случай низких температур, когда

.

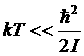В этом случае достаточно сохранить две первых члена суммы, поскольку именно они будут вносить наибольший вклад.

.

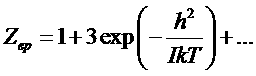В этом приближении свободная энергия будет равна

.

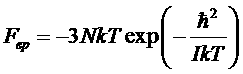Отсюда энтропия:

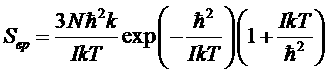
и теплоемкость

.

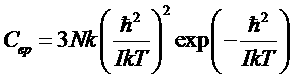Таким образом, вращательная энтропия и теплоемкость газа при T® 0 обращаются в ноль в основном по экспоненциальному закону. При низких температурах, следовательно, двухатомный газ ведет себя как одноатомный (говорят, что в этом случае вращательные степени свободы «заморожены»).

В общем случае произвольных температур сумма  может быть рассчитана только численно. На рис. приведен график cвр (в единицах k) как функции безразмерной величины .

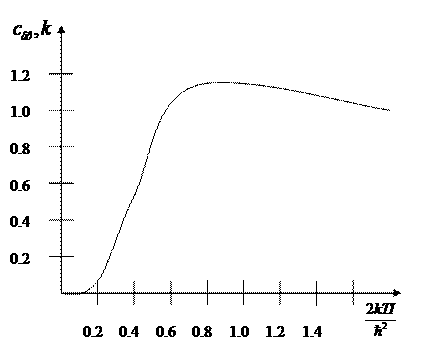
Рис. 2.2

Вращательная теплоемкость имеет максимум, равный 1,1 при 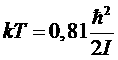, после чего асимптотически приближается к классическому значению 1.