Двухатомный газ. Колебания атомов

Колебательная часть термодинамических величин газа становится существенной при значительно более высоких температурах, чем вращательная, потому, что интервалы колебательной структуры велики по сравнению с интервалами вращательной структуры. В таблице приведены характерные колебательные температуры.

Мы будем считать, однако, температуру большой лишь настолько, чтобы были возбуждены в основном не слишком высокие колебательные уровни. Тогда колебания можно считать малыми и гармоническими, а уровни энергии определяются обычным выражением для гармонического осциллятора 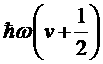. В случае ангармонических колебаний выражение для энергии будет значительно сложнее.

Вычислим колебательную статистическую сумму

.                              (*)

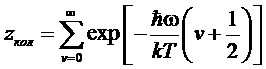Хотя при больших числах v колебания будут ангармоническими, но вследствие очень быстрой сходимости ряда суммирование можно распространить до бесконечности.

Сумма (*) представляет собой геометрическую прогрессию:

,

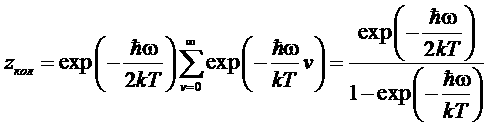откуда свободная энергия

,

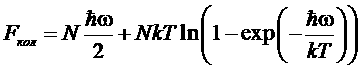энтропия

,

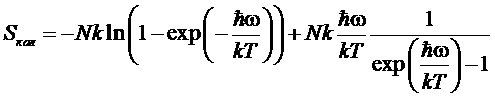энергия,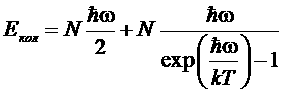

и теплоемкость.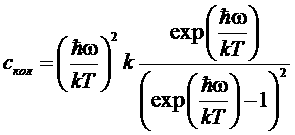

На рисунке изображен график зависимости  от .

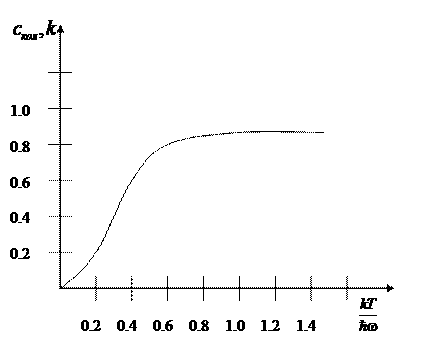
Рис. 2.3

При низких температурах () энтропия и теплоемкость стремятся экспоненциально к нулю:

,

,

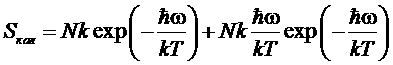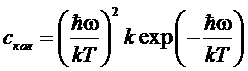а свободная энергия и энергия стремятся к постоянной величине.

При высоких температурах () имеем:

,

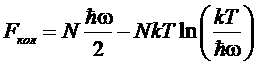чему соответствует постоянная теплоемкость .

Таким образом, полная теплоемкость двухатомного газа при температурах  (практически уже при ) равна

, .

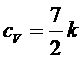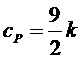Многоатомный газ. Свободную энергию многоатомного газа, как и двухатомного газа, можно представить в виде суммы трех частей- поступательной, вращательной и колебательной.

Благодаря большой величине моментов инерции многоатомных молекул (и соответственно, малости их вращательных квантов) их вращение можно всегда можно рассматривать классически. Эффекты квантования вращения могли бы наблюдаться лишь у метана CH4, где они должны появляться при температурах около 50K.

Многоатомная молекула обладает, в общем случае, тремя вращательными степенями свободы и большим числом колебательных степеней свободы. Если молекула обладает какими-либо осями симметрии, то повороты вокруг этих осей совмещают молекулу саму с собой и сводятся к перестановке одинаковых атомов. Например, если все атомы в молекуле расположены на одной прямой (линейная молекула), то она обладает, как и двухатомная молекула, всего двумя вращательными степенями свободы и одним моментом инерции.