Рассмотрим свободно-сочлененную полимерную цепь, состоящую из N сегментов. Будем предполагать, что отдельные сегменты цепи не взаимодействуют друг с другом посредством других сил, кроме тех, которые образуют саму цепь.
 |
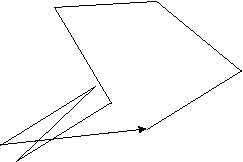Вектор RN, соединяющий концы этой цепи, описывается простым выражением:
.
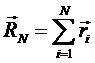Здесь i – порядковый номер сегмента цепи, 
- вектор, соединяющий начало и конец сегмента с номером i. Модули всех векторов одинаковы и равны длине одного сегмента l. Направления всех векторов случайны и независимы друг от друга. То есть полимерная цепь представляет собой клубок, характеризующийся величиной величиной 
, равной сумме большого числа случайных слагаемых. Для вывода формулы для характерного размера полимерного клубка введем величину 
, т.е. вектор, соединяющий начало первого сегмента цепи с концом сегмента с номером N-1:
, 
.
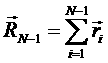Найдем теперь среднее расстояние между концами цепи. Учтем, что
,
поскольку все направления в пространстве равновероятны. Вычислим средний квадрат расстояния:
.
В результате получим:
,
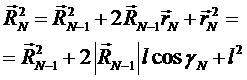где γN – угол между векторами и 
. В случае свободно-сочлененной полимерной цепи ориентация сегмента с номером N не зависит от ориентации остальных сегментов цепи. Следовательно, угол γN с одинаковой вероятностью принимает любое значение, а среднее значение его косинуса равно нулю. Таким образом, получим:
.
По индукции можно заключить, что
,
где L – контурная длина цепи.
Окончательно получим:
.
Верна ли эта формула при других модельных представлениях о полимерной цепи?
Рассмотрим, например, червеобразную молекулу. Если рассмотреть короткий участок такой молекулы, то на таком участке ее гибкость не проявляется, а молекула является жесткой. Введем понятие leff – это такая длина, участок меньше которой является жестким, а его длина равна контурной длине. В то же время участки с контурной длиной, больше чем leff ведут себя как последовательные сегменты свободно-сочлененной цепи. Величина leff еще называется сегмент Куна (по имени швейцарского ученого, впервые применившего статистическую механику к полимерам). Если контурная длина молекулы равна L, то очевидно, что эта молекула состоит из Neff = L/leff сегментов Куна. Тогда для определения размера цепи можно записать:
.
Это равенство можно рассматривать и как определение сегмента Куна. Длина сегмента Куна может варьировать от 1 нм до 100 нм для двойной спирали ДНК.
Распределение Гаусса для идеальной полимерной цепи
Из-за флуктуаций длина полимерной цепи постоянно меняется. Для доли конформаций (т.е. разных пространственных конфигураций) с данным R среди всех возможных конформаций можно записать выражение
.
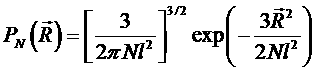Плотность вероятности для одной компоненты равна
.
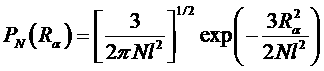Оба эти выражения представляют собой распределения Гаусса для R.
Поможем написать любую работу на аналогичную тему