Флуктуации изгиба длинных молекул

В обычных молекулах сильное взаимодействие атомов сводит внутримолекулярное тепловое движение лишь к малым колебаниям атомов около положений равновесия, практически не меняющих форму молекулы. Совсем иной характер имеет поведение молекул, представляющих собой  очень длинные цепи атомов (например, длинные полимерные углеводородные цепи). Большая длина молекулы, а так же сравнительная слабость сил, стремящихся удержать равновесную прямолинейную форму молекулы, приводит к тому, что флуктуационные изгибы молекулы могут стать весьма значительными, вплоть до скручивания молекулы. Большая длина молекулы позволяет рассматривать ее как своеобразную макроскопическую линейную систему, и для вычисления средних значений величин, характеризующих ее изгиб, можно применить статистические методы.

Будем рассматривать молекулы, имеющие вдоль своей длины однородное строение. Интересуясь лишь их формой, мы можем рассматривать такую молекулу как однородную сплошную нить. Форма этой нити определяется заданием в каждой ее точке вектора кривизны , направленного вдоль главной нормали к кривой и по величине равного ее обратному радиусу кривизны.

Испытываемые молекулой изгибы являются, вообще говоря,  слабыми в том смысле, что ее кривизна в каждой точке мала (ввиду большой длины молекулы это, разумеется, отнюдь не исключает того, что относительные смещения ее удаленных точек могут оказаться весьма значительными). Для малых значений вектора  свободная энергия изогнутой молекулы (отнесенная к единице ее длины) может быть разложена по степеням компонент вектора. Поскольку свободная энергия минимальна в положении равновесия (прямолинейная форма, = 0 во всех точках), то линейные члены в разложении отсутствуют, и мы получим

,   (*)

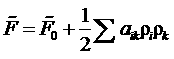где значения коэффициентов представляют собой характеристику свойств прямолинейной молекулы(к линии молекулы в данной ее точке) и ввиду предполагаемой однородности молекулы постоянны вдоль ее длины.

Вектор расположен в нормальной (к линии молекулы в данной ее точке) плоскости и имеет в этой плоскости две независимые компоненты. Соответственно этому совокупность постоянных  составляет двумерный симметричный тензор второго ранга в этой плоскости. Приведем его к главным осям и обозначим через  и  главные значения этого тензора (нить, в виде которой мы представляем себе молекулу, отнюдь не должна быть аксиально-симметричной по своим свойствам; поэтому  и  не должны быть равными). Выражение (*) примет в результате вид

,

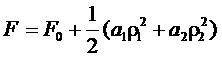где и - компоненты в направлении соответствующих главных осей.

Наконец, интегрируя вдоль всей длины молекулы, найдем полное изменение ее свободной энергии в результате слабого изгиба:

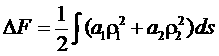  (127.2)

(s-координата вдоль длины нити). Величины  и ,  очевидно, непременно положительны.

Пусть  и  – единичные векторы вдоль направления касательных к нити в двух ее точках (точки a и b), разделенных участком длины s. Обозначим через  угол между этими касательными, т.е.

.

Рассмотрим сначала случай такого слабого изгиба, при котором угол  мал даже для удаленных точек. Проведем две плоскости, проходящие через и две главные оси тензора  в нормальной (в точке a) плоскости. При малых значениях  квадрат угла  может быть представлен в виде

,   (127.3)

где  и - углы поворота вектора  относительно вектора в указанных двух плоскостях. Компоненты вектора кривизны связаны с функциями  и  соотношениями

, ,

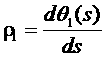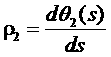и изменение свободной энергии при изгибе молекулы принимает вид

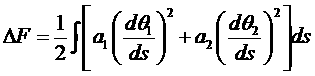.   (127.4)

         При вычислении вероятности флуктуации с заданным значением = и = при некотором определенном l надо рассмотреть наиболее полное равновесие, возможное при этих значениях  и . Другими словами, надо определить наименьшее значение свободной энергии, возможное при заданных и . Но интеграл вида

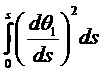
при заданных значениях функции на обоих пределах  имеет минимальное значение, если меняется по линейному закону. Покажем это. Задача минимизации интеграла относится к классу задач вариационного счисления. Если проводить аналогию с механикой, то выражение под интегралом есть функция Лагранжа, а s играет роль времени. Тогда запишем уравнение:

.

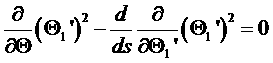Откуда получим:

.

Решением этого уравнения является линейная функция, которая при учете граничных условий принимает вид:

.

В результате интегрирования получим

.

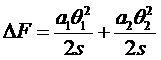При изотермическом процессе способность совершать работу характеризуется свободной энергией, следовательно, вероятность флуктуации в данном случае можно записать в виде

.

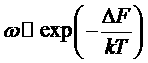В таком случае для средних квадратов обоих углов получаем

,

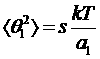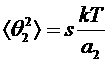
Средний же квадрат интересующего нас угла равен

.(«)

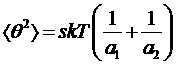Как и следовало ожидать, в этом приближении он оказывается пропорциональным длине отрезка молекулы между двумя рассматриваемыми точками. В выражении («) можно выделить величину с размерностью длины:

,

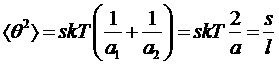где

,            .

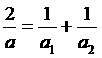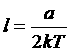Из выражения для свободной энергии легко видеть, что l имеет размерность длины.

Очевидно, как и ранее, что гибкость цепи определяется величиной . При малых величинах s получим:

.

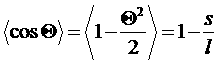Можно показать, что при достаточно больших величинах sсреднее значение быстро убывает с ростом sи равно

.

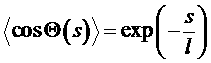Проанализируем это выражение. Рассмотрим короткий по сравнению с l участок цепи. При s<<l, т.е. угол флуктуирует около нуля, а концы короткого по сравнению с lучастка почти параллельны. В противоположном случае угол принимает почти любое значение, а память о направлении цепи на длине, намного большей l отсутствует.

Величина l называется персистентной длиной (от слова «стойкий»), или такой минимальной длиной участка, который способен сопротивляться изгибу. Поскольку память о направлении распространяется по обе стороны по цепи, то легко понять, что длина сегмента Куна должны примерно в два раза превышать персистентную длину l.