Как известно, некоторые полимеры (резина, каучук) обладают свойством высокой эластичности, т.е. способностью к большим обратимым относительным деформациям (для резины – до 8 раз). Оказалось, что необходимым условием высоко эластичности является наличие сшивок между полимерными цепями (вулканизация, вкрапления атомов серы), которые приводят к формированию полимерной сетки в веществе. Эта сетка не может течь, но может деформироваться.
Рассмотрим, как высокоэластичность проявляется на уровне отдельных полимерных молекул. Опишем поведение отдельной полимерной цепи, растягиваемой силой f. Первый такой эксперимент с молекулами ДНК проведен в 1992 году. Зададимся вопросом: как зависит координата конца вектора Rотf? Если рассмотреть идеальную полимерную цепь, состоящую из свободно-сочлененных участков длины l, в которой отсутствуют объемные взаимодействия, то неясно, откуда берется сила противодействия (по третьему закону Ньютона)? Например, в случае кристалла упругость связана с наличием сил взаимодействия (притяжения и отталкивания) между атомами (молекулами). В идеальной же макромолекуле таких сил нет, а изменение ее длины происходит за счет выпрямления и распутывания. Такая модель во многом сходна с идеальным газом.
При деформации вектора Rна величину ΔR совершается работа, равная
![]() .
.
На что идет такая работа, если растяжение происходит при постоянной температуре T? Очевидно, что в данном случае, работа идет на изменение энтропии цепочки (здесь проявляется аналогия со сжатием идеального газа).
Рассчитаем энтропию полимерной цепи, исходя из распределения Гаусса. Воспользовавшись формулой для энтропии
![]() ,
,
и считая, что величина Ω (в данном случае - число различных реализаций полимерной цепи при данной ее длине) пропорциональна величине PN, получим:
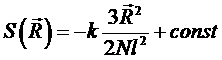 .
.
Тогда можно записать формулу для работы:
![]()
(знак минус в данном случае возникает из-за уменьшения энтропии) и силы
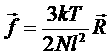 .
.
Фактически мы получили закон Гука для данного случая. Отметим, что модуль упругости в данном случае пропорционален 1/N, то есть очень мал для длинных полимеров.
Перейдем теперь к рассмотрению энтропийной упругости полимерной сетки, состоящей из идеальных субцепей (субцепь – элементарный кирпичик структуры полимерной сетки между двумя соседними сшивками). Пусть каждая субцепь состоит из N сегментов длины l. При растяжении сетки ее субцепи так же растягиваются, вследствие чего их энтропия уменьшается.
Допустим, что полимерная сетка представляет собой прямоугольный параллелепипед, который растягивается по осям в λx, λy и λz, соответственно. В результате получим для изменения энтропии в результате деформации сетки:
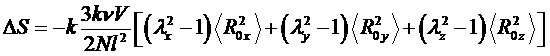 ,
,
где ν – число субцепей в единице объема, V – объем сетки, R0x, R0y, R0z – координаты какой-либо субцепи. Учтем теперь, что
![]() .
.
Учтем так же, что при недеформированном образце все три координатные направления были равноправны. Отсюда следует, что
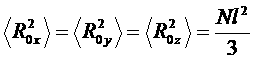 .
.
Окончательно получим для энтропии:
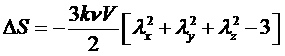 .
.
В это выражение не входят параметры отдельной субцепи N и l. Это указывает на универсальность выражения и является следствием идеальности субцепей.
Рассмотрим одноосное растяжение сетки вдоль оси x. При этом размеры сетки вдоль осей y и z изменяются свободно. Оказывается, что объем полимера при этом практически не меняется (он ведет себя как жидкость - при давлении 100 атм объем полимера изменяется лишь на 1%). Тогда имеем
![]() .
.
Тогда получим для энтропии:
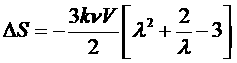 .
.
Растягивающая сила получается аналогично:
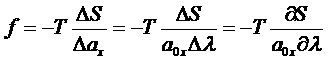 .
.
Определим напряжение:
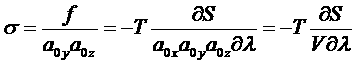 .
.
Окончательно получим:
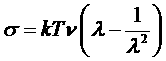 . (*)
. (*)
Формула является одной из основных в теории высокоэластичности полимерных пленок. Учтем, что если деформации невелики (λ близко к единице), то
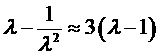 .
.
Величина же
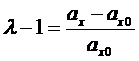
представляет собой относительную деформацию. Тогда получим для модуля Юнга полимерной сетки:
![]() .
.
Эта величина равна давлению идеального газа, концентрация молекул которого в три раза больше, чем концентрация сшивок в сетке. Чем меньше степень сшивки полимерного вещества, тем меньше его модуль Юнга. Замечательно, что выражение (*) описывает нелинейную упругость.
Поможем написать любую работу на аналогичную тему

