Отклонение  газов от идеальности

Ранее предполагалось, что молекулы газа не взаимодействуют друг с другом, однако во многих случаях такое взаимодействие должно учитываться. Для нейтральных атомов или молекул на малых расстояниях между ними преобладают силы отталкивания, а на больших – силы притяжения. Одним из распространенных потенциалов, хорошо описывающих взаимодействие нейтральных частиц, является потенциал Леннарда-Джонса

.

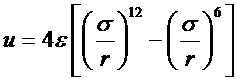Уравнение состояние идеального газа часто может применяться с достаточной точностью к реальным газам. Это приближение, однако, может оказаться недостаточным, и тогда возникает необходимость в учете реального газа от идеальности, связанного с взаимодействие молекул. Сделаем это, считая достаточно разреженным– на столько, чтобы пренебречь тройными, четвертными и прочими столкновениями молекул. Их взаимодействие осуществляется путем парных столкновений. Сначала рассмотрим одноатомный реальный газ. Движение его частиц можно рассмотреть классически, в этом случае энергия запишется в виде

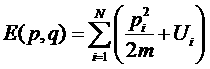
где первый член – кинетическая энергия N атомов газа, а U – энергия их взаимодействия друг с другом. У одноатомного газа U - функция только взаимных расстояний атомов. Статистический интеграл 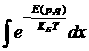  разбивается на произведение интеграла  по импульсам атомов и интеграла по их координатам. Последний имеет вид:  где интегрирование по каждому из dVi= dxidyidzi производится по всему занимаемому газом объему V. Для идеального газа U = 0 и этот интеграл равен VN. Свободную энергию можно вычислить по общей формуле

,

,

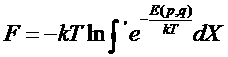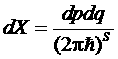 где S – число степеней свободы системы.

Для идеального газа свободная энергия может быть представлена в виде:

.

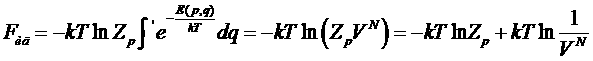Выражая константу Zp, получим:

.

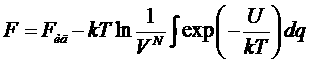Таким образом

.

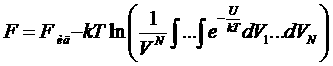Прибавим и вычтем из подынтегрального выражения единицу

.

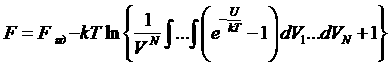Предположим, что газ не только достаточно разрежен, но и что количество его достаточно мало, так чтоб можно было считать, что в газе одновременно сталкивается не более одной пары атомов. Такое предположение не повлияет на общность, то в силу аддитивности свободной энергии известно из термодинамики, что она должна иметь вид: F = Nf(T,V/N). Поэтому формулы, выведенные для небольшого количества газа, автоматически справедливы для любых его количеств.

Взаимодействие между атомами не очень мало только тогда, когда соответствующие два атома находятся близко друг от друга, т.е. практически сталкиваются. Поэтому подынтегральное выражение заметно отличается от нуля только тогда, когда какие либо два атома находятся очень близко друг к другу. Согласно сделанному предположению этому условию может удовлетворять не более одной пары атомов. Причем эту пару можно выбрать из N атомов 0.5N(N–1) способами. Вследствие чего интеграл можно записать в следующем виде: 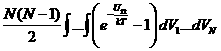 где U12 – энергия взаимодействия двух атомов (не имеет значения, каких именно) зависит от координат каких либо двух атомов. По всем остальным можно, следовательно, проинтегрировать, что дает VN-2 .

Кроме того, можно, конечно, написать N2 вместо N(N-1), N>> 1. Так как плотность газа мала – разложим ln(1+x)»x (x<<1).

Тогда имеем для свободной энергии:

.

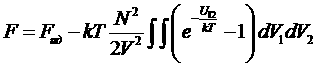Но U12 есть функция только взаимного расстояния обоих атомов, то есть разности их координат. Поэтому если ввести вместо координат каждого атома координаты их общего центра инерции и их относительные координаты, то U12 будет зависеть только от вторых (обозначим
dV = dxdydz). По координатам общего центра  инерции можно проинтегрировать. Это даст V. Окончательно:

,

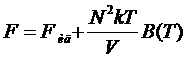где.                                   (*)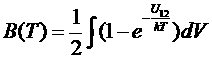

Отсюда находим давление

.

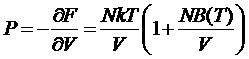Это уравнение состояния газа в рассматриваемом приближении. Те же формулы остаются в силе и для многоатомных газов. В этом случае потенциальная энергия зависит и от ориентации атомов. Однако углы всегда можно выбрать так, что константа, которую дает интегрирование по углам будет равна 1. Все полученные формулы имеют смысл при сходимости интеграла (*). Для этого необходимо, чтобы силы взаимодействия достаточно быстро убывали с расстоянием: на больших расстоянияхU12должно убывать быстрее, чем 1/r3. Это условие выполняется, так как силы взаимодействия между нейтральными атомами и дипольными молекулами убывают по закону U12 =1/r6.

Для одноатомных газов функция U(r) имеет вид:

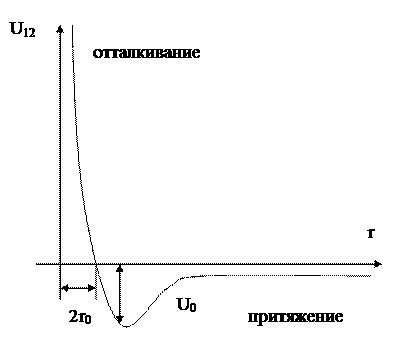
Рис. 3.1

На рисунке r0 представляет собой радиус атома, а U0 обычно невелико и составляет порядка kTc.

Определим знак B(T) для разных температур. При высоких температурах kT>>U0 во всей области r>2r0 имеем |U12|/kT<< 1 и подынтегральное выражение в B(T) близко к нулю. Поэтому значение интеграла  в основном определяется областью r< 2r0 , в которой U12/kT положительно и велико. В этой области, следовательно, подынтегральное значение положительно ®B(T)>0.

При низких температурах kT<<U0 основную роль в интеграле играет область r> 2r0, в которой теперь U12/kTотрицательно и велико по абсолютной величине (в области r< 2r0U12/kTвелико в любом случае!). Поэтому, при достаточно низких температурах B(T) должно быть отрицательно, причем зависимость B(T) от температуры в основном определяется экспоненциальным множителем: –exp(U0/kT).

Таким образом, B(T) должно проходить через ноль при некоторой температуре TB, называемой точкой Бойля. Полученное уравнение представляет собой первые два члена разложения давления по степеням 1/V:

.

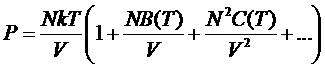Первый член разложения соответствует идеальному газу. Второй член получается при учете парного взаимодействия молекул, а в последующих членах должно участвовать взаимодействие молекул по 3, по 4 и т.д. Коэффициенты В и С … в разложении называют вторым третьим и т.д. вириальными коэффициентами.