Формула Ван-дер-Ваальса. Приведенное уравнение состояния

В газе взаимодействие между молекулами слабо. По мере его усиления свойства газа все ближе отклоняются от свойств идеальных газов, и, в конце концов, переходит в концентрированное состояние – жидкость. В жидкости взаимодействие между молекулами велико и, следовательно, свойства жидкости зависят от конкретного рода жидкости. Поэтому невозможно установить какие либо общие формулы, которые количественно описывали бы свойства жидкости. Можно, однако, найти некоторую интерполяционную формулу, качественно описывающую переход между жидкостью и газом. Эта формула должна давать правильные результаты в двух предельных случаях. Для разреженных газов она должна переходить в формулы идеальных газов. При увеличении плотности она должна учитывает ограниченную сжимаемость веществ. Для получения такой формулы исследуем более подробно исследовать отклонение от идеальности при высоких температурах.

Будем рассматривать одноатомный газ. По тем же соображениям формулы будут применимы и к многоатомным газам. Описанный ранее характер взаимодействия атомов газа позволяет определить вид первых членов разложения В(Т) относительно степени, обратной Т, при этом будем считать малым отношениеU0/kT<< 1.

Имея в виду, что U12 есть функция только расстояния r между атомами, имеем . Разбивая область интегрирования по dr на две части, запишем:

.

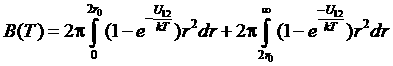Но при значениях r от 0 до 2r0 потенциальная энергия U12очень велика. Поэтому в первом интеграле можно пренебречь членом
exp(-U12/kT) по сравнению с единицей. Тогда интеграл становится равным положительной величине b = 16πr03/3 (если для одноатомного газа рассматривать r как радиус атома, то b есть его учетверенный объем). Во втором интеграле везде |U12|/kT<U0/kT<< 1. Поэтому можно разложить подынтегральное выражение по степеням U12/kT, ограничиваясь первым неисчезающим членом. Тогда второй интеграл становится равным

,

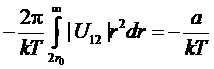где а – положительная постоянная. Таким образом, находим, что

.

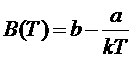Находим свободную энергию газа

.

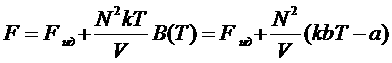Подставим в это выражение

,

которое мы получали раньше из статистической суммы для идеального газа.Тогда получим

.

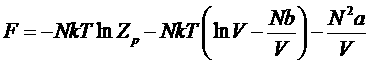При выводе формулы 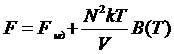 для свободной энергии газа мы предполагаем, что газ, недостаточного разрежен для того, чтобы считаться идеальным, однако имеет достаточно большой объем (так, что было можно пренебречь тройными и т.д. взаимодействиями), т.е. расстояние между молекулами значительно больше, чем их размеры. Можно сказать, что объем V газа, во всяком случае, значительно больше, чем Nb. Поэтому

.

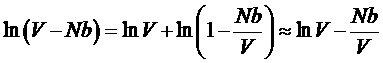Следовательно

 .                        (*)

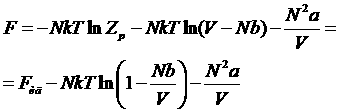В таком виде эта формула удовлетворяет поставленным выше условиям, т.к. при больших V она переходит в формулу для свободной энергии идеального газа, а при малых V она обнаруживает невозможность беспредельного сжатия газа (при V<Nb аргумент логарифма становится отрицательным). Зная свободную энергию, можно определить давление газа:

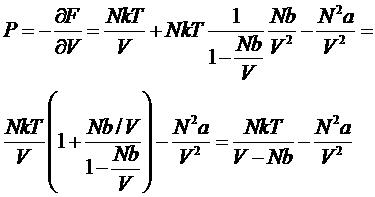
или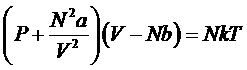

– это и есть искомое уравнения состояния реального газа – уравнение Ван-дер-Ваальса. Она является лишь одной из многих возможных интерполяционных формул. Ян Ван-дер-Ваальс вывел это уравнение в 1873 году (нобелевская премия 1910 года).

Энтропия реального газа из (*):

,              .

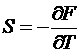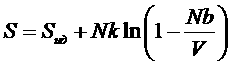Энергия E = F+ TS

.

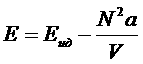Отсюда видно, что теплоемкость 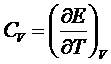  Ван-дер-Ваальсовского газа совпадет с теплоемкостью идеального газа (зависит только от Т) и может быть постоянной. Теплоемкость Ср, как легко убедиться, зависит не только от Т, но и от V и поэтому не может сводиться к постоянной. Второй член в Е соответствует энергии взаимодействий газа. Он отрицателен, т.к. преобладают силы притяжения. 

Приведенное уравнение состояния.

Запишем уравнение Ван-дер-Ваальса для одного моля газа:

.

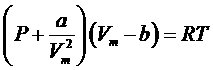Зависимости P(V) при постоянной температуре называются изотермами Ван-дер-Ваальса. Среди различных изотерм есть одна, которой соответствует критическое состояние, математически характеризуемое точкой перегиба. Приравнивая к нулю первую и вторую производные:

,                      ,

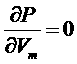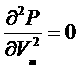получим критические параметры газа Ван-дер-Ваальса:

,      ,       .

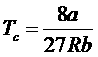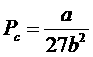Введем новые переменные:

,            ,             .

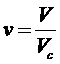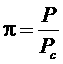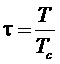Тогда уравнение Ван-дер-Ваальса может быть записано в этих новых безразмерных переменных:

.

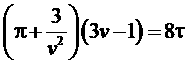Это уравнение называется приведенное уравнение Ван-дер-Ваальса. Его достоинство в том, что оно не содержит индивидуальных свойств газа, а значит, результаты, полученные на основе этого уравнения верны для всех газов (в заданном приближении).

На рисунке представлены зависимости  при различных значениях t (1 – 0.9, 2 – 1,0, 3 – 1.5).

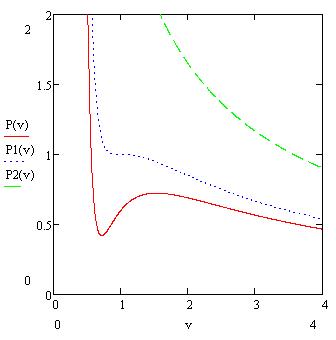
Кривая, соответствующаяt=1, является критической.

Утверждение о том, что все вещества подчиняются одному уравнению состояния, если это уравнение выразить через приведенные переменные, называется «закон соответственных состояний». Это закон первоначально был сформулирован Ван-дер-Ваальсом в 1873 году.