Термодинамические величины классической плазмы

Изложенный метод вычисления термодинамических величин идеального газа заведомо непригоден для газа, состоящего из заряженных частиц, взаимодействующих по закону Кулона, так как в этом случае входящие в формулу интегралы расходятся. Поэтому такой газ требует отдельного рассмотрения. Рассмотрим полностью ионизированный газ (плазма). Заряды его частиц будем обозначать посредствам zae, где индекс а отмечает различные сорта ионов (е - элементарный заряд, za- положительные или отрицательные числа). Пусть далее nа0 – число ионов а-го сорта в единице объема газа. Газ в целом электронейтрален:

.

Будем считать, что газ слабо отклоняется от идеальности. Для этого, во всяком случае, необходимо, чтоб средняя энергия кулоновского взаимодействия двух ионов (которая ~(ze)2/4πε0r, где r ~ n-1/3 – среднее расстояние между ионами) была мала по сравнению с кинетической энергией ионов (~kT). Таким образом, должно быть

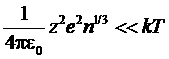 или .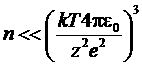

Ввиду электронейтральности плазмы среднее значение энергии кулоновского взаимодействия ее частиц, если бы все они были равномерно распределены в пространстве независимо друг от друга, обратилось бы в ноль. Поэтому первые поправки в термодинамических величинах плазмы (по сравнению с их значениями в идеальном газе) возникают только при учете корреляции между положениями различных частиц. С целью напоминать об этом, будем называть эти поправки корреляционными.

Начнем с определения поправки Eкорр в энергии плазмы. Как известно из электростатики, энергия электрического взаимодействия системы заряженных частиц может быть описана в виде половины суммы произведений зарядов на потенциалы поля, создаваемого в точках их нахождения всеми остальными зарядами.

В данном случае

,

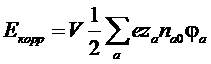 где φа – потенциал поля, действующего на ион а-го сорта со стороны остальных зарядов.

Вычислим эти потенциалы. Каждый из ионов создает вокруг себя некоторое (в среднем сферически симметричное) неравномерно заряженное ионное облако. Другими словами, если выбрать какой-либо ион в газе и рассматривать плотность распределения других ионов относительно данного, то эта плотность будет зависеть только от распределения r от центра. Обозначим плотность распределения ионов а-го сорта в этом ионом облаке посредствам nа. Потенциальная энергия каждого иона а-го сорта в электрическом поле данного иона есть zaeφ, где φ - потенциал этого поля:

.

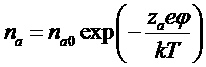Вдали от центра φ ® 0  поэтому na®nа0. Потенциал φ поля в ионном облаке связан с плотностью зарядов в нем () электростатическим уравнением Пуассона:

.                                        (*)

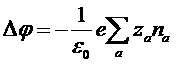Обе эти формулы составляют вместе систему уравнений самосогласованного электрического поля электронов и ионов. При сделанном нами предположении об относительной слабости взаимодействия ионов энергия zaeφ мала по сравнению с kT, и формулу можно приближенно переписать в виде:

.

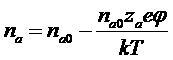Подставим это выражение в (*), и имея в виду условие , получим уравнение:

,

 где введено обозначение .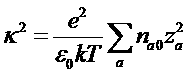

Величина  имеет размерность обратной длины. Центрально симметричное решение этого уравнения есть:

.

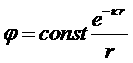В непосредственной близости от центра поле должно переходить в кулоновское поле данного заряда (величину, которую обозначим как zbе)

Те при r®0 должно быть 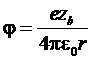® искомое распределение:

.

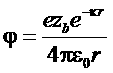Отсюда видно, что поле становится малым на расстояниях, больших по сравнению с . Поэтому эту длину можно рассматривать как определяющую размеры ионного облака, создаваемого данным ионом (ее называют дебаевским радиусом). Все производимые здесь вычисления, конечно, предполагают, что этот радиус велик по сравнению со средним расстоянием между ионами (покажем, что это условие совпадает с 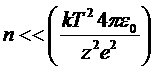). Разлагая потенциал в ряд при малых , найдем:

.

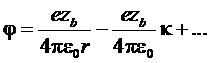Отрицательные члены обращаются при r® 0 в 0. Первый член есть кулоновского поля самого данного иона. Второй же член – потенциал, создаваемый всеми остальными ионами облака в точке нахождения данного иона. Это и есть та величина, которая должна быть представлена в формуле для Екорр

.

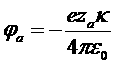Таким образом, мы получаем следующие выражения для корреляционной части энергии плазмы

.

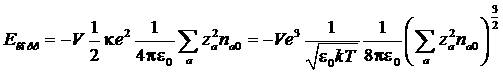Или введя полное число различных ионов в газе :

.

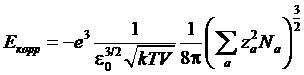Эта энергия обратно пропорциональна квадратному корню из температуры и объема газа. Интегрируя термодинамическое соотношение    (E = F + TS),

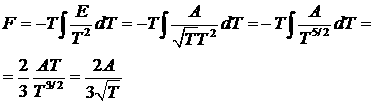
можно найти из Екорр соответствующую добавку к свободной энергии:

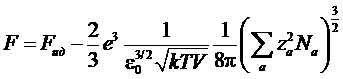
(постоянную интегрирования можно положить равной нулю, так как при T®¥ должно быть F = Fид).

Отсюда давление:

 ,      .

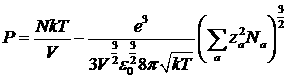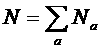Второе слагаемое предполагается малым по сравнению с первым, поскольку основным предположением было малое отклонение плазмы от идеальности.

Все это относится к классической невырожденной плазме. Может быть ситуация, когда температура плазмы настолько низка, что ее электронная компонента уже вырождена. При этом ионная компонента, благодаря большей массе ионов может быть еще далеко от вырождения. В этом случае существуют поправки к термодинамическим потенциалам, связанные с так называемым «обменным взаимодействием» электронов. Это чисто квантовый эффект, связанный с наличием спина у электрона.

Полученные формулы верны так же и для растворов, однако в них надо принимать во внимание, что между зарядами существует среда с диэлектрической проницаемостью ε.

Плазма всегда частично ионизирована. Формула Саха.