Вернемся опять к рассмотрению реальных газов и более подробно обсудим их поведение вблизи критической точки. Оказывается такое поведение имеет ряд существенных особенностей.
Как показывают экспериментальные данные при приближении к критической точке при фазовом переходе жидкость-газ, наблюдается резкое возрастание флуктуаций, что приводит к неограниченному увеличению вторых производных удельного термодинамического потенциала. Указанные аномально большие флуктуации реально наблюдаются на опыте, например, путем исследования рассеяния света средой, находящейся в критическом состоянии.
Происходящие при таких переходах явления получили название критических явлений. Экспериментальные и теоретические исследования критических явлений позволили сделать вывод о том, что в малой окрестности критической точки поведение параметров, характеризующих термодинамические свойства вещества, описывается простой степенной зависимостью
,
где малая величина x описывает близость температуры к критическому значению:
,
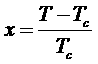а показатель степени l называется критическим индексом.
Экспериментально определенные значения критических индексов для различных веществ близки между собой. Между этими индексами для различных термодинамических величин, описывающих среду, установлены соотношения, позволяющие определять индексы одних величин через индексы других.
Определим критический индекс для коэффициента изотермической сжимаемости газа Ван-дер-Ваальса:
.
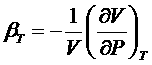Для одного моля газа Ван-дер-Ваальса уравнение состояния имеет вид
.
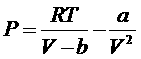Нахождение полных дифференциалов от правой и левой частей этого выражения дает
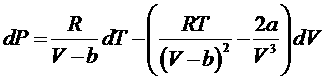
или
,
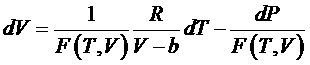где введено обозначение
.
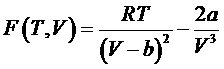Отсюда следует, что
.
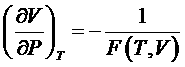Отсюда можно найти коэффициент 
:
.
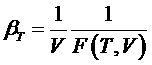Проведем разложение в ряд по температуре функции 
в окрестности критической точки при 
и 
, ограничившись только слагаемым первого порядка малости
.
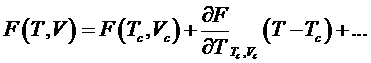Подстановка в первое слагаемое в правой части выражений для критических значений объема и температуры 
, 
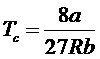дает:
.
Подставляя производную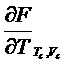 
в формулу для , получим
.
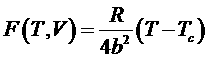Подстановка этой функции в выражение для коэффициента изотермической сжимаемости дает его зависимость от температуры в критической точке
.
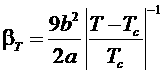Таким образом, для газа Ван-дер-Ваальса при его критическом переходе из газообразного состояния в жидкое, коэффициент изотермической сжимаемости стремится к бесконечности. При этом критический индекс для этого термодинамического параметра l = 1.
Как показывают экспериментальные данные, критический индекс коэффициента изотермической сжимаемости реальных газов близок к полученному значению и имеет величину: l = 1,22 ± 0,02.
Несовпадение полученного для газа Ван-дер-Ваальса значения критического индекса с экспериментально измеренными значениями связано с тем, что при проведенном рассмотрении нами не учитывались сильные флуктуации, возникающие в критической точке. В непосредственной близости от этой точки возникают макроскопические корреляции флуктуаций, радиус действия которых становится существенно больше радиуса действия межмолекулярных сил. При этом величины флуктуаций параметров состояния среды (например, её плотности) достигают самих значений этих параметров. Все это приводит к некоторому несовпадению полученного значения критического индекса с данными экспериментов.
Из ранее полученной формулы для флуктуации объема следует, что
.
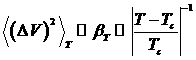То есть, при приближении температуры к критической средний квадрат флуктуаций объема неограниченно возрастает. В действительности он не будет возрастать до бесконечности, поскольку при выводе флуктуации объема было использовано разложение в ряд для возвращающей квазиупругой силы, а так же квадратичность энергии осциллятора. Поскольку в критической точке вторая производная от давления по объему так же равна нулю, то необходимо производить разложение в ряд до третьего слагаемого, которое не навно нулю. Тогда флуктуации объема будут стремиться к некоторому большому числу, но не к бесконечности.
Кеннет Вильсон был награжден в 1982 г. Нобелевской премией по физике «за теорию критических явлений в связи с фазовыми переходами».
Критическая опалесценция – резкое усиление рассеяния света чистыми веществами в критических состояниях, а так же растворами жидкостей или газами при достижении ими критических точек. Объяснена в 1907 году Смолуховским, показавшим, что при критической температуре сжимаемость вещсства сильно возрастает, в связи с чем энергия теплового движения его частиц становится достаточной для внезапного сильного увеличения микроскопических флуктуаций плотности. В результате практически прозрачная среда при температурах выше и ниже критической в критическом состоянии становится мутной.
Мутная среда, это среда в которой рассеяние света сопровождается значительным рассеянием, влияющим на условия распространения, вследствие чего нарушается прозрачность среды.
Поможем написать любую работу на аналогичную тему