Основы теории переноса тепла были заложены французским математиком Фурье (1768-1830) в первой четверти XIX века. Хотя Фурье и исходил из неправильной теории теплорода, т.е. предполагал, что теплота была каким-то веществом, он получил правильное математическое выражение для плотности теплового потока. Плотностью потока теплоты называется вектор j, совпадающий по направлению с направлением распространения теплоты и численно равный количеству теплоты, проходящему в одну секунду через площадку в один квадратный сантиметр, перпендикулярную к направлению потока теплоты. Закон Фурье для неподвижной среды можно записать в следующем виде:
![]() ,
,
где ![]() - коэффициент теплопроводности (Вт/м×К).
- коэффициент теплопроводности (Вт/м×К).
Выведем уравнение баланса тепла сначала для одномерного случая.
 Пусть имеется неограниченная среда, в которой возникает поток теплоты в направлении, параллельном оси x. В одномерном общем случае свойства среды и величины, характеризующие тепловой поток, могут меняться в том же направлении. Кроме того, они могут меняться во времени. Поэтому плотность потока теплоты j
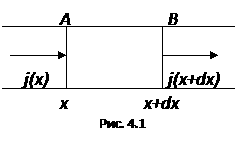
следует рассматривать как функцию координаты xи времени t : j = (x, t). Выделим мысленно в среде бесконечный цилиндр с образующими, параллельными оси x, и рассмотрим бесконечно малый участок такого цилиндра АВ длиной dx(рис. 4.1). Пусть S — площадь поперечного сечения цилиндра. Количество теплоты, поступающее в цилиндр АВ завремя dtчерез основание А с координатой x, равно j (x)Sdt. Количество теплоты, уходящее за то же время через основание В, будет j(x + dx)Sdt. Так как через боковую поверхность цилиндра теплота не поступает, то полное количество теплоты, поступающее за время dtчерез рассматриваемый участок цилиндра, равно
Пусть имеется неограниченная среда, в которой возникает поток теплоты в направлении, параллельном оси x. В одномерном общем случае свойства среды и величины, характеризующие тепловой поток, могут меняться в том же направлении. Кроме того, они могут меняться во времени. Поэтому плотность потока теплоты j
следует рассматривать как функцию координаты xи времени t : j = (x, t). Выделим мысленно в среде бесконечный цилиндр с образующими, параллельными оси x, и рассмотрим бесконечно малый участок такого цилиндра АВ длиной dx(рис. 4.1). Пусть S — площадь поперечного сечения цилиндра. Количество теплоты, поступающее в цилиндр АВ завремя dtчерез основание А с координатой x, равно j (x)Sdt. Количество теплоты, уходящее за то же время через основание В, будет j(x + dx)Sdt. Так как через боковую поверхность цилиндра теплота не поступает, то полное количество теплоты, поступающее за время dtчерез рассматриваемый участок цилиндра, равно
![]() .
.
Но эту теплоту можно представить в виде dM×cvdT, где dM = ρSdx- масса цилиндра АВ, cv — удельная теплоемкость, dТ — повышение температуры. Приравнивая оба выражения и производя сокращение, получим
![]() . (*)
. (*)
Закон Фурье для одномерного случая можно записать в виде:
![]() .
.
Подставляя выражение для плотности потока тепла в (*), получим:
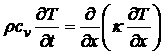 .
.
Это уравнение называется уравнение теплопроводности. Коэффициент теплопроводности в общем случае зависит от температуры или от координат, но в частном случае, когда эта величина постоянна, имеем:
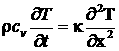 ,
,
или
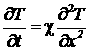 ,
,
где введено обозначение
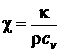 .
.
Постоянная χ называется температуропроводностью среды.
Уравнение теплопроводности легко обобщается на случай трехмерного пространства:
![]() , или
, или
![]() .
.
Однако тепло может переноситься не только за счет теплопроводности, но и за счет движения среды как целого. В таком случае можно записать для плотности потока тепла:
![]() .
.
Второе слагаемое представляет собой плотность потока тепла, возникающую за счет переноса массы. Покажем для общего случая, что второе слагаемое действительно есть плотность потока тепла, обусловленная движением среды. Рассмотрим аддитивную величину φ, которая переносится вместе со средой в направлении оси x. Обозначим через![]() плотность величины φ (т.е. величина φ, заключенная в единице объема вещества). Рассмотрим цилиндрический объем с площадью поперечного сечения S, по которому движется среда со скоростью v вдоль оси x. Тогда за время dtчерез поперечное сечение пройдет величина φ, равная:
плотность величины φ (т.е. величина φ, заключенная в единице объема вещества). Рассмотрим цилиндрический объем с площадью поперечного сечения S, по которому движется среда со скоростью v вдоль оси x. Тогда за время dtчерез поперечное сечение пройдет величина φ, равная:
![]() .
.
Деля на Sи dt, получим для плотности потока величины φ выражение:
![]() .
.
Или в трехмерных координатах:
![]() .
.
Тогда можно записать уравнение баланса тепла в виде
![]() .
.
Наконец, в среде могут оказаться источники теплоты. Например, теплота может выделяться в результате прохождения электрического тока или радиоактивного распада. Такие источники мы не принимали во внимание. Чтобы их учесть, введем величину qV, равную количеству теплоты, выделяемому источниками в единице объема среды в одну секунду. Тогда уравнение баланса тепла запишется в виде:
![]() .
.
Соотношения, во многом аналогичные, можно записать и для переноса частиц. Аналогом закона Фурье для переноса частиц выступает закон Фика:
![]() ,
,
где j– вектор плотности потока числа частиц, D – коэффициент диффузии частиц в среде (м2/с). Вывод уравнения баланса числа частиц во многом аналогичен. Для одномерного случая полное число частиц, поступающее за время dt через рассматриваемый участок цилиндра, равно
![]() .
.
Но изменение числачастиц можно представить в виде, где dN = Sdxdn. Приравнивая оба выражения и производя сокращение, получим
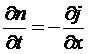 . (*)
. (*)
Закон Фика для одномерного случая можно записать в виде:
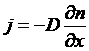 .
.
Окончательно получим:
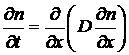 .
.
Для постоянного коэффициента D имеем:
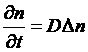 .
.
Это уравнение можно аналогичным образом обобщить на случай движущейся среды и источников частиц (например, это могут быть химические реакции или радиоактивный распад):
![]() .
.
Это уравнение называется уравнение баланса числа частиц.
Зависимости коэффициентов переноса от параметров в различных средах!
Поможем написать любую работу на аналогичную тему

