Броуновское движение. Уравнение Ланжевена

Частный случай такого движения был описан ботаником Г. Броуном в 1827 году, когда он в микроскоп наблюдал за движением мельчайших частиц пыльцы. Однако характер этого движения был понят только в XX веке.

Рассмотрим движение крупных частиц в термически однородной среде типа газа или жидкости. Термин «крупные частицы» в данном случае означает, что частицы макроскопически наблюдаемы, т.е. размер их порядка R~ 10-4 см (для зеленого света l ~ 0,5×10-4 см). Этот размер и с молекулярной точки зрения является большим.

Например, для воздуха при нормальных условиях среднее расстояние между молекулами ~ 0,5×10-7 см, для жидкости – на порядок меньше.

Будем считать, что известны форма, размер, масса и т.д. броуновской частицы (БЧ), а также все свойства среды.

Рассмотрим облака БЧ, полагаем, что они не взаимодействуют друг с другом. Поэтому мы вправе рассматривать какую-либо одну БЧ.

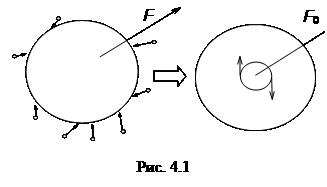
Такая крупная частица взаимодействует сразу с большим числом частиц среды и под действием общей равнодействующей совершает два типа случайных блужданий (рис.4.1):

а) флуктуации общей величины приводят к трансляционному броуновскому движению,

б) флуктуации момента равнодействующей силы – к вращательному броуновскому движению.

Математически эти процессы во многом эквивалентны, а значит, ограничимся первым типом.

Рассмотрим пространственно однородную систему (потенциал внешней силы ) и в ней – одну броуновскую частицу. Т.к. направления x, y,zэквивалентны, исследуем одномерное броуновское движение вдоль оси x.

Выделим из силы F, действующей на броуновскую частицу, ту ее часть, которая существовала бы и в отсутствие флуктуаций. Эта регулярная часть силыF представляет собой не что иное, как силу вязкого трения (которая нам известна).

Например, для сферических частиц радиуса R согласно формуле Стокса:

,

h – коэффициент вязкости; v, p – скорость и импульс.

Тогда точное уравнение движения БЧ можно записать в виде:

- уравнение Ланжевена (1908 г.),

- случайная часть силы, действующей на БЧ. В среднем она равна нулю:

<F(t)> = 0.

Проанализируем временные интервалы взаимодействия БЧ с окружением:

– время соударения частицы с частицей среды t ~ 10-12c
(для R ~ 10-4 см);

– время между отдельными взаимодействиями t' ~ 10-16¸ 10-17c;

– время исчезновения информации (релаксации) о начальном состоянии tМ ~ G-1~ 10-10c.

        При сравнении величин этих интервалов обращают на себя внимание характерные соотношения:

t'<<tиt<<G -1.