Уравнение баланса энтропии

Уравнение баланса энтропии в общем виде можно записать следующим образом:

,

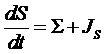где JS – поток энтропии через границы системы, Σ – производство энтропии (источник энтропии). Следствием второго начала термодинамики является то, что в изолированной системе энтропия не может убывать. Это означает, что производство энтропии не может быть отрицательно:

.

Рассмотрим производство энтропии на примере диффузии газа в сплошной среде. Два объема V1 и V2 соединены капилляром и представляют вместе изолированную систему. Поскольку система изолирована, то поток энтропии через ее границы равен нулю. В таком случае производство энтропии может быть определено так:

,

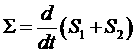где S1 и S2 энтропии вещества, находящегося в объемах. Каждую из этих величин можно записать на основе первого начала термодинамики:

,

.

Здесь мы пренебрегли изменением объема, а, следовательно, и работой, совершаемой одной системой над другой. Тогда получим:

.

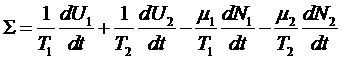Но ввиду изолированности системы суммарная внутренняя энергия и число частиц сохраняются:

,

.

Отсюда получим:

.

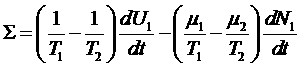Определим производные следующим образом:

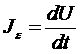 – поток энергии,

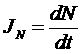- поток числа частиц.

Преобразуем величины в скобках, имея в виде, что отклонение от равновесия в каждой системе мало:

,

.

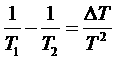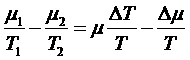Введем так же поток тепла:

.

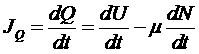В результате получим для производства энтропии:

.

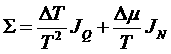Видим, что производство энтропии может быть представлено в виде суммы произведений потоков и соответствующих им сил:

.

Заметим, что выбор потоков (или сил) произволен – можно было выбрать поток энергии.

Поскольку система изолирована, то производство энтропии в ней – величина положительная. В данном случае это можно проиллюстрировать тем, что тепло переходит от более нагретого тела к менее нагретому, или частицы движутся в область с меньшим химическим потенциалом.

В условиях, когда допустимо представление о локальном равновесии можно построить последовательную феноменологическую термодинамику необратимых процессов. Свойства неравновесной системы при этом определяются локальными термодинамическими потенциалами, которые зависят от пространственных координат и времени только через характеристические термодинамические параметры, для которых справедливы уравнения термодинамики.

Рассмотрим теперь в произвольной системе малый объем и запишем аналогично производство энтропии для этого объема. Для простоты примем, что процессы переноса происходят только вдоль оси x. Тогда объем будет представлять собой цилиндр площадью Sи длиной Δx. Тогда имеем:

,

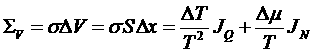где σ – плотность производства энтропии. Преобразуем:

.

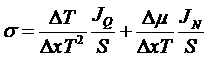Переходя к пределу, имеем:

.

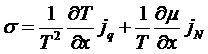Видим, что плотность производства энтропии может быть представлена в виде суммы произведений плотностей потоков и соответствующих им сил. В данном случае силы будут представлять собой градиенты:

,

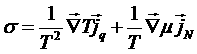или

.