Основные положения линейной неравновесной термодинамики

В равновесном состоянии термодинамические силы , потоки  и производство энтропии равны нулю. Поэтому при малых отклонениях от равновесия естественно положить линейную связь между потоками и силами:

.

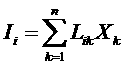Коэффициенты  в этом линейном законе называются кинетическими коэффициентами. Причем диагональные коэффициенты  определяю «прямые» явления переноса, а недиагональные коэффициенты  - перекрестные или сопряженные процессы. Эти соотношения можно записать в матрично-векторном виде:

.

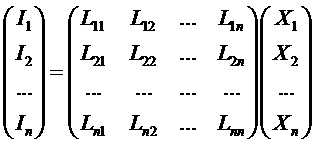Для плотностей потоков можно записать аналогичные выражения:

.

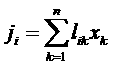Например, по закону теплопроводности Фурье градиент температуры вызывает поток теплоты , по закону Фика градиент концентрации вызывает диффузию , , по закону Ома градиент потенциала вызывает ток ,  и т.д. Наряду с этими прямыми процессами переноса возникают и перекрестные процессы. Например, при существовании градиента температуры кроме переноса теплоты может происходить и перенос массы (термодиффузия). Такие перекрестные процессы характеризуются недиагональными коэффициентами . Так, плотность потока массы может быть пропорциональная градиенту температуры и т.д.

Не все коэффициенты  являются независимыми. В 1931 году Ларс Онсагер, исходя из инвариантности микроскопических уравнений движения относительно изменения знака времени (временная симметрия) и из представления о неравновесном состоянии системы, вызванном внешними силами, как крупной флуктуации равновесной системы, установил, что в области линейности необратимых процессов матрица кинетических коэффициентов симметрична:

.

Это соотношение называют соотношение взаимности Онсагера.

Это соотношение приводит к тому, что число независимых величин в матрице кинетических коэффициентов становится меньше. Число диагональных коэффициентов равно n, а число независимых перекрестных коэффициентов равно:

.

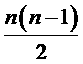Теорема Пригожина. Рассмотрим систему, в которой имеются два потока и две соответствующие им силы:

,

.

Пусть в такой системе реализована ситуация, когда одна из сил (X1) зафиксирована, т.е. поддерживается каким-либо способом. В результате поток J2 в стационарном состоянии станет равным нулю, поскольку сила X2будет подстраиваться до тех пор, пока два слагаемых в этом потоке не будут компенсировать друг друга. Запишем производство энтропии для такой системы:

.

Найдем экстремум величины Σ, для чего возьмем производную от Σ по X2:

.

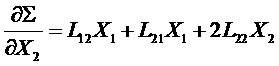Принимая во внимание соотношение взаимности Онсагера, имеем:

.

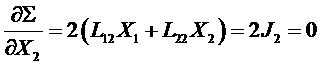Видим, что в стационарном состоянии имеет место экстремум величины Σ. Можно показать, что это минимум, поскольку вторая производная положительна. Таким образом, теорему Пригожина можно сформулировать в следующем виде:

Если хотя бы одна из термодинамических сил зафиксирована, то в стационарном состоянии система стремится к минимуму производства энтропии.

Эта теорема применима только к линейным системам.

Принцип Кюри

В термодинамике существует принцип Кюри для изотропных систем, свойства которых одинаковы во всех направлениях: потоки и движущие силы разной тензорной размерности не могут быть связаны друг с другом. Так, например, причина-скаляр не может вызвать векторный поток.

Таким образом, согласно принципу Кюри линейные соотношения между потоками и силами и принцип симметрии кинетических коэффициентов справедливы только для потоков и сил одинаковой тензорной размерности.

По тензорной размерности необратимые процессы можно разделить на три группы:

1. скалярные - химические реакции, источники тепла и числа частиц;

2.                              векторные - диффузия и теплопроводность в сплошной фазе, вязкое взаимодействие между фазами;

3.                              тензорные - вязкое взаимодействие в сплошной фазе, деформации.

Движущей силой химических реакций является химическое сродство, а потоком - скорость реакции. Например, для реакции:

поток (скорость реакции) можно записать в виде:

.

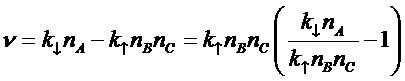Коэффициенты, называемые константами скорости реакции, связаны уравнением детального баланса:

,

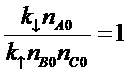где , ,  концентрации соответствующих веществ в равновесии.

Тогда поток можно записать в виде:

,

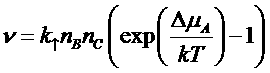где 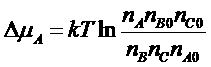 - разность химических потенциалов исходных веществ и продуктов реакции. Эта величина называется так же «сродство реакции».

В то же время в асимметричных системах запрет на связь потоков разной размерности отсутствует. Это можно продемонстрировать на примере термоэлектрических явлений.