Вывод соотношений взаимности Онсагера из теории флуктуаций

Докажем важное свойство коэффициентов Lik, называемое соотношениями взаимности Онсагера. Для доказательства соотношений недостаточно соображений феноменологической термодинамики и следует использовать микроскопическую теорию.

Основная гипотеза, на которой базируется теория Онсагера, заключается в том, что макроскопическое слабо неравновесное состояние системы можно рассматривать как крупную флуктуацию. То есть градиенты температуры, концентрации и других величин, существующие в макроскопической системе, подчиняются тем же законам, что и градиенты, возникающие благодаря флуктуациям.

Будем характеризовать замкнутую систему набором параметров ai, равных нулю в равновесном состоянии. Так как в состоянии равновесия энтропия системы максимальна, то вблизи от равновесия имеем равенство:

,

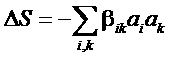где неотрицательно определенная матрица коэффициентов βik может быть выбрана симметричной βik = βki.С другой стороны, вблизи от равновесия скорость изменения параметров так же должна быть малой величиной, так как в состоянии равновесия эта величина должна обращаться в нуль. Допустим, что вблизи от равновесия скорости  являются малыми первого порядка по ai:

.

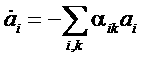Считая энтропию функцией параметров ai, находим для производной по времени dS/dt, которая для замкнутой системы совпадает с производством энтропии выражение

.

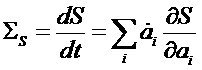Дальнейшее доказательство основано на том, что первый множитель в правой части отождествляется с потоком, а второй – с сопряженной ему термодинамической силой:

, .

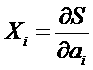Найдем связь между потоками и силами. Из выражения для энтропии имеем:

,

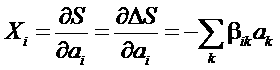Откуда, вводя обратную матрицу, получим

.

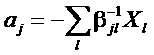Подставим это выражения в формулу для потоков:

.

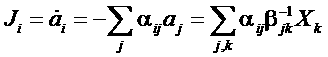Для кинетических коэффициентов, следовательно, получим:

.

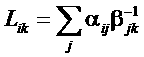Уравнение для потоков можно переписать в виде:

.

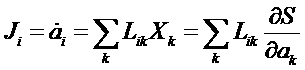Рассмотрим произведение

,

где τ – промежуток времени, малый по сравнению с характерными временами изменения параметров ak. Тогда эти величины можно разложить в ряд по времени:

.

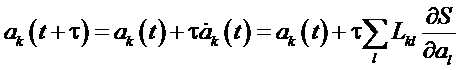Задание зачения ak(t)не определяет однозначносостояния системы в момент времени t+τ, так как существует еще ряд параметров al(t)(l≠k),и тем более не определяет значениеak(t+τ), так как при заданном ak(t)возможен ряд процессов, ведущих к разным значениям ak(t+τ).

Найдем среднее значение следующего выражения

.

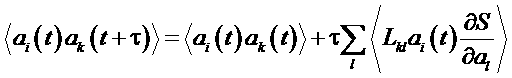Для расчета воспользуемся ранее полученной функцией распределения для флуктуаций:

.

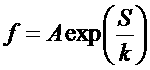Тогда получим:

.

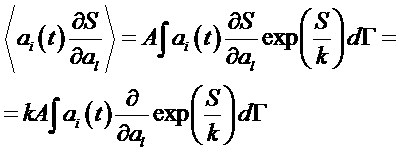Проинтегрируем это выражение по частям. Для этого примем во внимание, что элемент объема в фазовом пространстве для флуктуаций имеет вид:

.

Тогда получим:

.

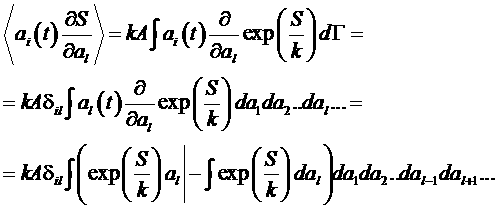Ввиду быстрой сходимости экспоненциальной функции, получим:

.

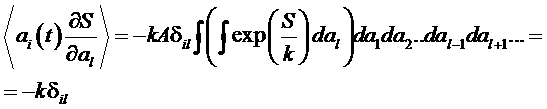Таким образом, получим:

.

Аналогично можно получить соотношение:

.

Если параметры ai, ak таковы, что они не меняются при изменении всех скоростей, то в силу симметрии уравнений механики по отношению к операции отражения времени безразлично, какую из величин мы берем в более ранний, а какую в более поздний момент времени. Следовательно

.

Отсюда следует

.

Это соотношение справедливо и в том случае, если обе величины и пропорциональны нечетной степени скорости и меняют знак при отражении времени.