Уравнение Мастера.Диффузия тяжелого газа в легком

Простейшим процессом, описывающим причинную связь между событиями, является марковский процесс. Марковский процесс характеризуется тем, что переход из состояния в момент времени  в состояние в момент времени  не зависит от предыстории системы. При этом переходы внутри двух последовательных временных интервалов происходят независимо друг от друга.

Для марковских процессов справедливо основное кинетическое уравнение. Рассмотрим некоторое состояние системы . Система может перейти в новое состояние, совершив скачок . Вероятность прямого перехода из состояния  в единицу времени в состояние обозначим через, а вероятность обратного перехода из состояния  в состояние  будет . Отсюда сразу следует уравнение

   .        (*)

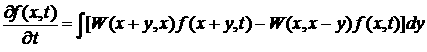Первое слагаемое в (*) характеризует прямые переходы ,  а второе обратные .

Уравнение (*) называется основным кинетическим уравнением (уравнение Мастера). Основное кинетическое уравнение представляет собой уравнение баланса для плотности вероятности каждого состояния . Первый член в правой части уравнения (*) соответствует возрастанию вероятности из-за переходов из других состояний , а второй  - уменьшению вероятности из-за переходов в другие состояния.

Для дискретных величин аналогом уравнения мастера является уравнение Паули:

.

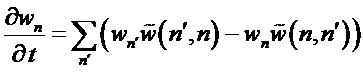В этом уравнении – вероятность перехода из состояния n’ в состояние n в единицу времени, - убыль за секунду вероятности обнаружить систему в состоянии n за счет переходов во все другие состояния системы n’, - обратный процесс. Это уравнение так же называют уравнением кинетического баланса. Можно показать, что вероятность переходов обладает свойством симметрии:

.

Это уравнение еще называется уравнением детального баланса. Оно является следствием законов сохранения.

Заметим, что, вообще говоря, не все случайные процессы в природе являются марковскими. Существуют еще процессы с памятью, в которых информация о прошлых состояниях может сохраняться в системе достаточно долгое время.

Вывод уравнения Фоккера-Планка из уравнения мастера.

Значительную категорию кинетических явлений составляют процессы, в которых средние изменения величин (от которых зависит функция распределения) в каждом элементарном акте малы по сравнению с их характерными значениями. Времена релаксации таких процессов велики по сравнению с временами элементарных актов, составляющих их микроскопический механизм; в этом смысле такие процессы можно назвать медленными.

Типичный пример такого рода дает задача о релаксации по импульсам небольшой примеси тяжелого газа в легком (который сам по себе предполагается находящимся в равновесии). Ввиду малой концентрации тяжелых частиц, их столкновениями друг с другом можно пренебречь и рассматривать их столкновения лишь с частицами основного (легкого) газа. Но при столкновении тяжелой частицы с легкими ее импульс испытывает лишь относительно малое изменение.

Будем для определенности говорить именно об этом примере и выведем кинетическое уравнение, которому удовлетворяет в таком случае функция распределения частиц примеси по импульсам, f(t, p).

Обозначим через ω(р, q)d3q отнесенную к единице времени вероятность изменения импульса р → р-q тяжелой частицы при элементарном акте - ее столкновении с легкой частицей. Тогда кинетическое уравнение для функции f(t, p) запишется в виде

,

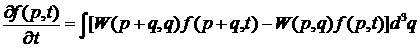где справа стоит разность между числом частиц, поступающих (в 1 с) в заданный элемент импульсного пространстваd3p и покидающих его за то же время. Согласно сделанным предположениям, функция ω(р, q) быстро убывает с увеличением q, так что основную роль в интеграле играют значения q, малые по сравнению со средним импульсом частиц. Это обстоятельство позволяет произвести в подынтегральном выражении разложение

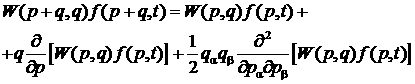
В результате кинетическое уравнение примет вид

,

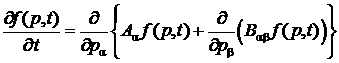где 

, .

Выражение в правой части (21.2) имеет вид дивергенции в импульсном пространстве,, от вектора

.

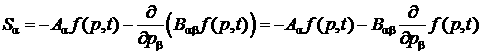Если коэффициент постоянен или почти постоянен, то это откуда-то должно следовать! Превращение из тензора в скаляр тоже не так очевидно, поскольку не совсем ясно, почему при эта величина должна обращаться в ноль.

Другими словами, полученное уравнение имеет, как и следовало, вид уравнения непрерывности в импульсном пространстве; тем самым автоматически соблюдается сохранение числа частиц при процессе. Вектор же S является плотностью потока частиц в импульсном пространстве.

Согласно приведенным формулам коэффициенты в кинетическом уравнении выражаются через средние характеристики столкновений, и в этом смысле их вычисление представляет собой механическую задачу. Фактически, однако, нет необходимости в раздельном вычислении коэффициентовAαиBαβ; они могут быть выражены друг через друга из условия обращения потока в нуль в статистическом равновесии. В данном случае равновесная функция распределения есть

,

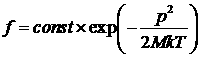где М — масса частиц тяжелого газа, а Т — температура основного (легкого) газа. Подстановка этого выражения в уравнение S = 0 дает

.

Таким образом, кинетическое уравнение принимает вид

.             (*)

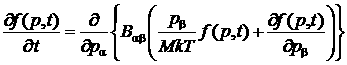Единственный вектор, от которого могут зависеть коэффициенты Bαβ , — импульс тяжелых частиц р. Но если скорости этих частиц, р/М, в среднем малы по сравнению со скоростями легких частиц (при чем тут скорости?), то при столкновениях их можно считать неподвижными; в этом приближении величины Вαβ не будут зависеть от р. Другими словами, тензор Вαβ сведется к постоянному скаляру В:

,               

а уравнение (*) примет вид

.                                 (**)

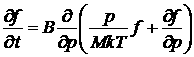Обратим внимание на формальное сходство полученных уравнений (*) с уравнением диффузии во внешнем поле, в особенности наглядное в записи (**), а так же с уравнением Фоккера-Планка. Описываемые уравнением (*) процессы можно назвать диффузией в импульсном пространстве, причем В играет роль коэффициента диффузии.

Ясно поэтому, что уравнение такого же типа будет справедливо и для функций распределения f по другим переменным, если только выполнены условия, лежащие в основе вывода: относительная малость изменения величин в элементарных актах и линейность по f интегрального оператора, выражающего изменение функции благодаря этим актам.