Причины необратимости в макросистемах

Рассмотрим вопрос о необратимом характере процессов релаксации в макроскопических системах. Как известно, законы, определяющие эволюцию микроскопической системы во времени, инвариантны по отношению к изменению знака времени как в классической, так и в квантовой механике. Это значит, что все микропроцессы принципиально обратимы, т.е. при надлежащем изменении условий (например, при изменении направлений начальных скоростей) любой микропроцесс может протекать, как в прямом, так и в обратном направлении, проходя через одни и те же промежуточные состояния.Возникает вопрос: каким образом статистическая физика, основанная на обратимых во времени законах микропроцессов, может приводить к необратимым законам макроскопических процессов, в частности, к описанию процессов релаксации и к закону возрастания энтропии в замкнутых системах?

Исторически после работ Больцмана по вычислению возрастания энтропии в изолированной газовой системе были сформулированы два наиболее важных возражения против кинетической теории.

Теорема возврата (парадокс Пуанкаре-Цермелло).Теорема возврата утверждает, что за достаточно большое время фазовая траектория в фазовом пространстве, изображающая поведение системы, вернется в область, сколь угодно близкую к некоторой начальной точке этой траектории.Доказательство этой теоремы основано на свойстве несжимаемости газа изображающих точек – теореме Лиувилля.

Таким образом, эволюция состояния макроскопической системы столь же обратима, как и микроскопические процессы. В частности, любое неравновесное макроскопическое состояние рано или поздно должно повториться, как бы ни было велико отклонение от равновесия. Это противоречит представлениям о том, что поведение системы необратимо во времени.

Парадокс Лошмидта. Уравнения движения механики обратимы во времени, поэтому можно представить себе последовательность состояний эволюции системы, и, в равной мере (в силу обратимости уравнений движения), обратную последовательность состояний. Состоянию zi сопоставляется энтропия Si. Тогда, если в одной из последовательностей состояний энтропия возрастает, то в другой она убывает. Почему же тогда энтропия в замкнутой системе только возрастает?

Энтропия не изменяется.Докажем, что если вычислить энтропию на основе функции распределения, являющейся решением уравнения Лиувилля, то такая энтропия в замкнутой системе не будет изменяться со временем.

Рассмотрим производную по времени от энтропии изолированной системы и покажем, что она равна нулю

.

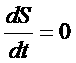Воспользуемся известной формулой для энтропии

.

Будем считать, что функция распределения подчиняется уравнению Лиувилля:

.

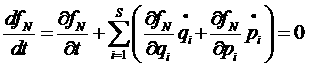Далее будем подразумевать, что по повторяющимся индексам производится суммирование. Найдем производную от энтропии:

.

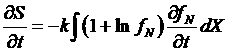Частная производная берется, поскольку энтропия не может зависеть от координат и импульсов (интеграл по ним определенный). Далее получим:

.

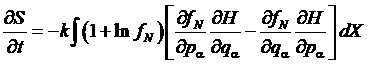Введем обозначение

.

Учтем, что выполняются следующие равенства:

, .

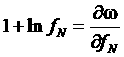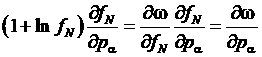Тогда получим:

.

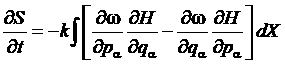Под знаком интеграла мы получили скобку Пуассона от функций ω и H. Теперь заметим, что

.

Следовательно, многомерный интеграл содержит одномерные, которые легко берутся:

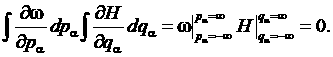
Равенство интеграла нулю есть следствие того, что нормированная функция распределения обращается в ноль на бесконечности.

Каким же образом разрешить сформулированные парадоксы?

Рассмотрим два примера:

1.     В сосуде, разделенном перегородкой на две одинаковые части, газ первоначально находится в одной половине. Мы удаляем перегородкуи наблюдаем расширение газа в пустоту – происходит релаксация в координатном пространстве.

2.     В холодный газ впускается пучок горячих молекул, имеющих почти одинаковые скорости v. Спустя некоторое время благодаря соударениям газ «максвеллизируется», и установится равновесное распределение молекул по скоростям.

В соответствии с теоремой Пуанкаре-Цермелло мы можем утверждать, что спустя некоторое время первоначальное неравновесное состояние должно повторяться со сколь угодно большой точностью, т.е. в первом примере газ вновь собраться в одну половину сосуда, а во втором примере должен снова сформироваться пучок молекул со скоростью v.

Однако такая абстрактно-теоретическая концепция, связанная с теоремой возврата, имеет для больших флуктуаций весьма отдаленную связь с действительностью, так как времена возврата для столь сильных отклонений от равновесия, как в двух рассмотренных примерах, оказываются невообразимо большими, во много раз большими возраста Вселенной.

Грубую оценку времени возврата можно получить следующим образом. Пусть в объемеV находится N молекул газа. Будем понимать под возвратом повторение начального состояния каждой молекулы с точностью до Δv по скорости и Δx по координате. Этой точности соответствует объем ΔГ фазового пространства газа, равный

,

в то время как всему набору состояний газа с фиксированной кинетической энергией E соответствует объем

,

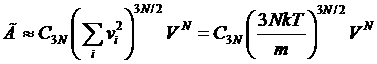где .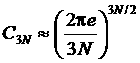

Прежде, чем вернуться с заданной точностью в исходное положение, изображающая точка должна пройти число состояний, равное по порядку величины Г/ΔГ. Так как время свободного пробега молекулы τ имеет порядок

,

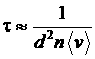то для времени возврата получим оценку:

.

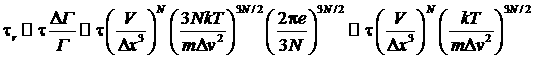Если задать, равными 10% их первоначальных значений расстояния и скорости, то получим

.

Для 1 см3 газа при нормальных условиях эта величина экспоненциально больше возраста Вселенной.

Таким образом, абстрактно теоретическая обратимость сочетается с практической необратимостью макроскопических процессов, если речь идет о сколь-нибудь существенных отклонениях от равновесия.

Уравнения типа Фоккера-Планка, диффузии и другие описывают процессы, идущие только с возрастанием энтропии. Возникает вопрос, на каком этапе вывода уравнений переноса возникает необратимость? В случае уравнения Фоккера-Планка такой гипотезой является предположение о марковском характере процесса (марковским называется процесс, в котором будущие состояния не зависят от прошлых – именно такой процесс был использован ранее при выводе уравнений переноса). Можно сформулировать и другой вариант такого рассмотрения: в равновесии в замкнутой системе равновеликие площади на гиперпространстве постоянной энергии равновероятны. Неравновесные системы таким свойством не обладают. Следовательно, в неравновесных системах должен существовать некоторый механизм перемешивания, т.е. переход к равномерному распределению точек в фазовом пространстве.

Одним из первых ученых, понявших важность такого свойства, был Н.С.Крылов. Проиллюстрируем идеи Крылова на примере идеального газа.

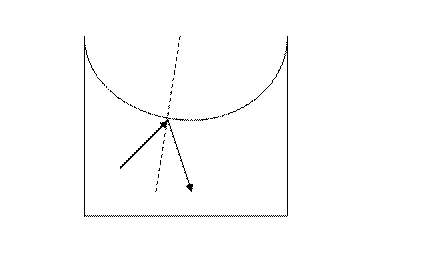
Я.Г. Синай рассмотрел задачу столкновения двух шаров и показал, что эта задача сводится к столкновению материальной точки с выпуклой стенкой. При этом оказалось, что в системе возникает неустойчивость, которая заключается в том, что любое малое начальное отклонение траектории одного из шаров приводит к увеличению этого отклонения после столкновения. В данном случае это означает, что движение такой материальной точки будет необратимо. С течением времени вся фазовая плоскость будет занята траекториями. Поскольку фазовое пространство ограничено, то в нем будет происходить явление, называемое перемешиванием.

Идеи Больцмана по обоснованию кинетической теории были существенно продвинуты Эренфестом. Однако наиболее трудным в проблеме обоснования статистической физики оказался вопрос о том, как возникает близкое к равновесному распределение состояний системы на поверхности постоянной энергии. Анализ, проведенный Крыловым, показал, что в основе понимания природы статистических законов лежит не свойство эргодичности динамической системы, а свойство перемешивания и связанная с ним локальная неустойчивость. Анализ Крылова показал так же, что в уравнениях динамики не содержится какого-либо механизма огрубления (усреднения), даже если динамика является квантовой. Процедура огрубления является дополнительным приемом, который привносится в описание природы извне.

Покажем, как эти парадоксы разрешаются на основе современной теории. Отметим, что проявления статистических свойств в системе вовсе не обязательно, чтобы она состояла из большого числа частиц. Эти свойства могут проявиться в системе, состоящей из двух частиц.

Прежде всего, отметим, что теорема Пуанкаре о возвратах не имеет никакого отношения к появлению статистических свойств в системе. Возвраты существуют как при условно периодическом движении, так и при стохастическом движении. В последнем случае времена последовательных возвратов (циклов) являются случайной последовательностью, а величина их для систем из малого числа частиц также мала. Необратимость проявляется не в том, что система не может вернуться близко к исходному состоянию, а в ином ее свойстве. Рассмотрим фазовую каплю правильной формы и будем следить за изменением формы ее границ со временем. В устойчивом случае (в отсутствии перемешивания) поверхность капли изменяется не очень сильно, в то время как в случае локальной неустойчивости поверхность капли быстро приобретает необычайно сложную и запутанную форму.

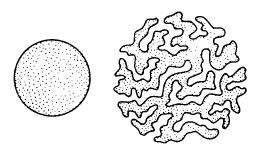
Рис.

Необратимость связана именно с этой формой. Интуитивно ясно, что вероятность возврата капли в свою старую форму столь же мала, как и вероятность возврата для большого числа частиц. Пренебрежение этой вероятностью, эквивалентное некоторому огрублению, и приводит к необратимости.

Теперь проследим за тем, почему нельзя, как заметил Больцман в ответе Лошмидту, повернуть все частицы в обратном направлении, и, тем самым, заставить систему перейти из более вероятного состояния в менее вероятное. Рассмотрим выходящий из малой области Δ0 пучок траекторий. Рассмотрим так же через некоторое, не слишком большое время область Δ~Δ0и те траектории, которые, выйдя изΔ0, попадают в областьΔ. Будем считать, что Δесть масштаб огрубления в фазовом пространстве. Это означает, что индивидуальный характер траекторий внутри Δдля нас потерян. Поэтому внутри области Δмы не можем отличить те траектории, которые совершили путьΔ →Δ0, от траекторий, идущих по другим путям. Следовательно, мы не можем повернуть траектории системы, вышедшие из Δ0, в обратную сторону. Точнее, мы не можем повернуть только те траектории, которые вышли из Δ0. Мы поворачиваем все траектории, находящиеся в Δ, т.е. огромное число других траекторий. Именно в этом месте и начинает работать свойство перемешивания системы, которое необходимо для последнего утверждения.

При локальной неустойчивости через короткое время (время перемешивания) в области Δнаходится много чужих траекторий, не вышедших из Δ0. Таким образом, огрубление приводит к потере информации об индивидуальных траекториях в области огрубления Δв момент их достижения этой области (и тем самым в любой последующий момент времени), а перемешивание приводит к заполнению области огрубления за конечное время траекториями, о которых теряется информация. Наконец, важным является то, что перемешивание заполняет область огрубления траекториями, прошедшими почти из любой области фазового объема. Поэтому в смешении информации участвует доля порядка траекторий, в которых равномерно представлены состояния почти всего фазового объемаΔ~Δ0, а не малой его части. Такая ситуация, обеспечиваемая перемешиванием, делает механизм потери информации экстремальным и устойчивым.

Таким образом, неустойчивость и огрубление являются необходимыми предпосылками для существования необратимых процессов в природе.

Следовательно, энтропия, определенная в статистической физике и энтропия, определенная в термодинамике, не всегда эквивалентны. Энтропия из термодинамики (Клаузиуса) требует понятия «равновесие». Однако, если равновесия нет, то нельзя ввести не только энтропию, но и температуру, а так же другие термодинамические параметры.