На практике вместо дисперсии истинной ошибки se2, значение которой не известно, используется ее оценка, рассчитываемая на основе фактических значений ошибки еt согласно следующей формулы (см. (1.32), (2.19)):
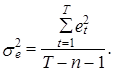
Обоснованность такой замены можно подтвердить, показав, что M=se2, т. е. математическое ожидание дисперсии фактической ошибки, определенной на основании известных оценок МНК параметров эконометрической модели, равно дисперсии ее “истинной” ошибки.
Заметим, что векторы значений фактической и “истинной” ошибки связаны следующим соотношением:
e=у –Х×a=Х×a+e–Х×=
=e–Х×(Х¢Х)–1×Х¢×e=×e=G×e, (2.57)
где ET – единичная матрица размера Т´Т и G=ET–Х×(Х¢Х)–1×Х¢ – симметрическая полуопределенная идемпотентная матрица, обладающая согласно ее определению следующим свойством*:
Gk=G, k=2, 3,... (2.58)
Из (2.57) следует, что расчетные значения фактической ошибки еt линейной эконометрической модели могут быть выражены в виде линейных комбинаций неизвестных значений истинной ошибки et. В этом случае сумму квадратов значений фактической ошибки можно представить в следующем виде:
![]() (e¢e)=e¢G¢Ge=e¢Ge. (2.59)
(e¢e)=e¢G¢Ge=e¢Ge. (2.59)
При выводе выражения (2.59) учтено, что G – симметрическая идемпотентная матрица.
Найдем математическое ожидание левой и правой частей выражения (2.59).
M= M=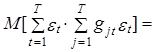
![]() tr(G), (2.60)
tr(G), (2.60)
где tr(G)=![]() – след матрицы G, представляющий собой сумму ее диагональных элементов (сумму элементов главной диагонали);
– след матрицы G, представляющий собой сумму ее диагональных элементов (сумму элементов главной диагонали); ![]() =se2 – дисперсия “истинной” ошибки модели.
=se2 – дисперсия “истинной” ошибки модели.
При выводе выражения (2.60) также учтено, что M=0, если t¹j в силу независимости разновременных значений ошибки et.
След матрицы G может быть определен с учетом свойств этой характеристики. В связи с этим напомним, что:
а) след арифметической суммы матриц равен сумме следов каждой из них
tr(G)= tr(ET)– tr; (2.61)
б) следы произведений матриц AB и BA равны между собой, естественно при условии, что оба произведения AB и BA матриц A и B существуют.
Тогда, учитывая, что матрица Х¢Х имеет размер (п+1)´(п+1), получим
tr=tr=trEп+1, (2.62)
где Eп+1 – единичная матрица размера (п+1)´(п+1).
Поскольку в силу формы единичных матриц trET=Т и trEп+1= п+1, то из выражения (2.60) вытекает, что несмещенная оценка дисперсии истинной ошибки модели se2 определяется на основании следующего выражения:
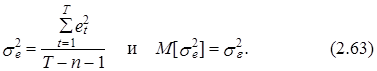
Поможем написать любую работу на аналогичную тему

