Оценка последствий неправильного выбора состава независимых переменных модели

В данном разделе рассмотрим особенности влияния на качество параметров эконометрической модели ошибок, допущенных на этапе содержательного анализа при выборе состава независимых переменных (факторов). В разделе 2.2.3 было отмечено, что при обосновании модели могут иметь место ошибки двух видов: выбрана неправильная форма функционала f(a, xt) и неверно определен состав ее независимых переменных. Такие ошибки называют ошибками спецификации модели – ошибка спецификации формы уравнения модели и ошибка спецификации матрицы Х. Ошибка спецификации первого вида часто приводит к появлению автокорреляционных взаимосвязей во временном ряду фактической ошибки модели еt. Это в определенной степени является свидетельством того, что и ее “истинная” ошибка et  не обладает  свойствами процесса “белого шума”, поскольку в такой ситуации следует ожидать невыполнение стандартных условий (2.21) и (2.22).

Ошибка спецификации матрицы Х  может быть обусловлена разными причинами. Во-первых, в модель могут быть не включены некоторые “существенные” факторы, во-вторых, включены несущественные факторы. Возможна также комбинация этих причин. Рассмотрим последствия, к которым приводят различные варианты ошибки спецификации матрицы Х.

Предположим, что вместо “истинной” эконометрической модели с матрицей значений независимых факторов Х

у=Хa+e                                    (2.67)

была  сформирована модель с матрицей , отличной от Х,

у=b+x,                                   (2.68)

где b – вектор коэффициентов модели (2.68).

Для модели (2.68) на основе МНК были найдены оценки параметров согласно известному выражению

b=(¢)–1×¢у.                           (2.69)

где b  – вектор оценки параметров модели b.

Подставив в (2.69) вместо вектора у  правую часть из выражения (2.67), получим

b=(¢)–1×¢Хa+(¢)–1×¢e.                  (2.70)

Из этого результата непосредственно вытекает, что, если столбцы матрицы  и ошибка модели (2.67) независимы, то

M=G×a,                                      (2.71)

где G=(¢)–1×¢ – матрица, столбцами которой являются оценки коэффициентов моделей следующего вида:

где х it   – значение i-го фактора матрицы X в момент t; i=1,2,...,n; – значение j-го фактора матрицы в момент t;  j=1,2,...,k. При этом n и k  – количества независимых факторов в матрицах X и  соответственно.

Из выражения (2.71) вытекают следующие результаты:

1.   Предположим, что матрица  отличается от матрицы Х  только отсутствием последних r столбцов. Иными словами,  модель (2.68) отличается от модели (2.67) тем, что в нее не вошли переменные х k+1,t , х k+2,t,..., хnt, где п–k=r – т. е. =, Х=, где хi =¢. В этом случае матрица G будет иметь следующий вид:

G =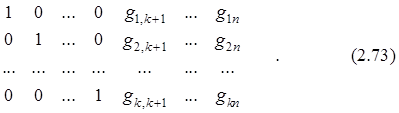    

Заметим, что матрица G размера k´n будет образована объединением единичной матрицы Еk  размера k´k и матрицы Gr размера k´r,  элементами которой являются коэффициенты моделей типа (2.72), в которых в качестве зависимых  переменных   выступают   не   включенные  в  матрицу  факторы х k+1, хk+2,..., хn.  С учетом вида матрицы  очевидно, что

G=.                                    (2.74)

где

Еk=(¢)–1×¢

Подставив матрицу G из выражения (2.74) в выражение (2.71), получим соотношение, связывающее математические ожидания параметров модели (2.68) с “истинными” параметрами модели (2.67)

Таким образом, оценка j-го коэффициента модели (2.68) оказывается смещенной по отношению к истинному значению j-го коэффициента модели (2.67), j=1, 2,...,k, и величина этого смещения определяется следующим выражением:

Заметим, что коэффициенты gj,m, т=k+1,..., п; зависят от ковариаций, включенных в модель (2.68) первых k независимых факторов и невключенных в нее последних r независимых факторов модели (2.67), поскольку gj,m= где j=1,2,...,k, т=k+1,..., п.

В самом деле, если в качестве независимых факторов моделей (2.67) и (2.68) использовать центрированные переменные со значениями  (cм. выражение (1.13)), то gj,m= представляет собой числитель ковариации факторов х j   и  х m.

Смещение оценок коэффициентов (2.70) можно интерпретировать также как перераспределение силы воздействия невключенных факторов на оставшуюся их совокупность.

2.   Предположим, что матрица  образована присоединением дополнительных r столбцов-значений переменных х jt, j=1, 2,..., r,  корреляционно не связанных с переменной уt   (не оказывающих влияние на зависимую переменную). Для облегчения выкладок будем считать, что все переменные рассматриваемых моделей центрированы. В таком случае матрицу , в которой отсутствует единичный столбец, можно представить в следующем виде:

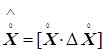
где D – матрица размера Т´r, образованная значениями переменных . Тогда согласно выражениям (2.69) и (2.74) получим

b=¢=

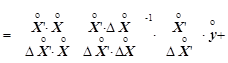f(e)=

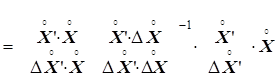×a+f(e)G×a+f(e),      (2.89)

где f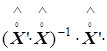(e)=e.

Рассмотрим математическое ожидание вектора b. Поскольку факторы , значения которых образуют присоединенную матрицу D, переменная  и ошибка e независимы, то       M=M=, т. е. вектор оценок коэффициентов при присоединенных факторах является нулевым.

Из этого результата вытекает, что математическое ожидание произведения матриц D¢ и  также образует нулевую матрицу соответствующего размера. Таким образом,

M=0.                                     (2.78)

С учетом (2.78) матрицу G из выражения (2.77) можно представить в следующем виде:

G =   ¢×         0     –1      ¢×   =    Еп  ,              (2.79)

                                           0    D¢×D            0               0

где Еп – единичная матрица размера п´n, и нулем обозначена матрица размера r´n, состоящая из нулевых элементов.

Полученные результаты свидетельствуют, что оценки коэффициентов эконометрической модели с добавленными несущественными факторами являются несмещенными оценками коэффициентов “истинной” модели. При этом математические ожидания оценок коэффициентов при добавленных факторах равны нулю. Кроме того, присоединенные факторы и основные факторы модели попарно независимы.

Полученные результаты позволяют посмотреть на проблему отбора факторов для эконометрической модели под другим углом зрения. Несущественные факторы должны характеризоваться слабыми (незначительными) корреляционными взаимосвязями с основными независимыми переменными. На это может указать значение коэффициента множественной детерминации между фактором хi  и остальным набором переменных. Если его значение, рассчитанное для i-го фактора согласно выражению (2.54) является незначимым по критерию Фишера (выражение (2.66)), то есть все основания полагать, что этот фактор является несущественным. Однако при этом необходимо быть уверенным, что все остальные факторы способны объяснить изменчивость переменной уt в достаточно полной мере.