МЕТОДЫ ОЦЕНКИ КОЭФФИЦИЕНТОВ ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ C НЕСТАНДАРТНЫМИ ОШИБКАМИ

В данной главе рассматриваются основные подходы к оценке коэффициентов эконометрических моделей, свойства которых отличаются от “стандартов”, определенных в главе II условиями (2.21)–(2.23). Иными словами, у “нестандартной” ошибки ее ковариационная матрица может быть отлична от диагональной матрицы Cov(e)¹se2×Е, что является следствием существования корреляционных взаимосвязей между ее разновременными значениями на интервале (1, Т), дисперсия ошибки может не обладать свойством постоянства, se2¹const (гетероскедастичность ошибки) или ошибка e может быть связана с одной или несколькими независимыми переменными эконометрической модели хi.

Первый случай (наличия автокорреляционных взаимосвязей в ряду ошибки et, t=1,2,..., Т) формально может быть выражен следующим условием:

                         Соv(e)=W=se2×S, S¹Е,                          (3.1)

где  W – ковариационная матрица ошибок модели; S – матрица коэффициентов автокорреляции модели, отличная от единичной; se2=const.

В общем случае матрица S может быть представлена в  следующем виде:

                    S =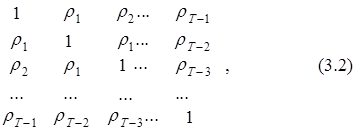 

где, напомним, что rk – коэффициент автокорреляции рядов ошибки et  и  et–k, k-го порядка, значение которого рассчитывается для k=1,2,... по формуле:

Во втором случае ковариационная матрица ошибки имеет следующий вид:

   Сov(e)=W=

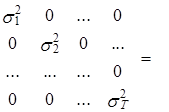
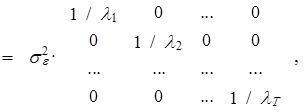                                    (3.4)

где формально s12¹s22 ¹...¹sТ2, т. е. дисперсия ошибки не постоянна, а    se2 – постоянный множитель, lt – переменные коэффициенты, t=1,2,..., Т. Выражение (3.4) характеризует свойство ошибки, известное в эконометрике как гетероскедастичность остатков. Иными словами, ряд ошибки характеризуется нестационарностью второго порядка, т. е. непостоянством второго центрального, а, значит, и начального моментов на интервале (1,Т), в то время как первый момент – математическое ожидание ошибки – принимает на этом интервале постоянное значение, равное нулю.

В эконометрических исследованиях теоретически возможна ситуация, когда оба рассмотренных случая встречаются одновременно, т. е. когда в ряду ошибки имеются автокорреляционные зависимости и ее дисперсия непостоянна.

Третий случай характеризуется нарушением условия (2.23), что означает отличие от нуля ковариации хотя бы одной независимой переменной хi  и ошибки модели e  или, что то же самое, отличие от нуля их парного коэффициента корреляции, cov(хit, et)¹0,

Нарушение условий (2.21) и (2.22) приводит к тому, что оценки коэффициентов эконометрических моделей, полученные на основе “классических” методов МНК и ММП, теряют некоторые свои “качества”. Прежде всего это относится к свойству эффективности оценок, полученных при ограниченных объемах выборки.

Нарушение условия (2.23), как это следует из выражения (2.10), приводит к потере оценками коэффициентов модели свойства несмещенности. Заметим, что если условия (2.21)–(2.23) не выполняются при Т®¥, то оценки коэффициентов не обладают свойствами асимптотической эффективности и несмещенности (состоятельности).

Такая ситуация, в свою очередь, заставляет эконометриков искать определенные подходы, приемы получения “качественных” оценок параметров эконометрических моделей и при свойствах их ошибок, отличных от тех, которые были определены стандартными условиями (2.21)–(2.23).

Данные подходы и приемы обычно базируются на так называемых обобщенных методах оценивания – обобщенном МНК (ОМНК) и обобщенном ММП (ОММП), на использовании при получении оценок параметров моделей так называемых “инструментальных переменных”. Рассмотрим особенности этих подходов более подробно.