Рассмотрим основные последствия нарушения условия (2.21) для оценок параметров эконометрической модели, полученных с использованием “классических” методов оценивания, например, МНК.
Как было показано в разделе 2.1, применение обычного МНК для определения коэффициентов эконометрической модели при условии W¹se2×Е в этом случае приводит к следующим результатам (см. выражения (2.9) и (2.15)):
– оценка вектора параметров модели является случайной величиной, которую можно представить в следующем виде:
a=a+(X¢X)–1X¢×e; (3.5)
– ковариационная матрица этих оценок определяется следующим выражением:
Cov(a)=(X¢X)–1X¢WX(X¢X)–1=se2(X¢X)–1X¢SX(X¢X)–1¹se2(X¢X)–1.(3.6)
Из выражений (3.5) и (3.6), в частности, вытекает, что вектор а является несмещенной оценкой вектора истинных значений параметров эконометрических моделей a и в случае конечных объемов выборки детерминированных исходных данных (Т – конечно) и асимптотически несмещенной оценкой при стохастических исходных данных, поскольку в этих случаях при соблюдении условия M=0 имеем M=Mx]=a (см. выражение (2.36)).
Однако из (3.6) также следует, что при конечных объемах выборки оценки, найденные с использованием обычного МНК, являются неэффективными. При этом отметим, что неравенство (3.6) обусловлено не только различиями матриц (X¢X)-1X¢SX(X¢X)–1 и (X¢X)–1, но и тем обстоятельством, что используемая на практике оценка дисперсии модели se2
может быть смещенной в силу существующих зависимостей в ряду ошибки (между разновременными значениями ошибки).
Вместе с тем можно показать, что при Т®¥ оценки обычного МНК и в этих условиях при выполнении некоторых предположений являются состоятельными и асимптотически эффективными. Для этого перепишем выражение (3.6) в следующем виде:
Cov (a) =
Из (3.7), в частности, вытекает, что элементы матрицы Cov(a)®0, и вектор a является состоятельной оценкой вектора a при Т®¥, если в этом случае матрицы 
являются конечными и положительно определенными.
Можно показать, что эти предположения выполняются, если
а) наименьший характеристический корень матрицы (X¢X) неограниченно возрастает при Т®¥, что влечет за собой выполнение условия:
plim(X¢X)–1=0;
б) наибольший характеристический корень матрицы S ограничен по величине для всех Т.
В частности, в случае гетероскедастичной ошибки последнее условие означает, что в выражении (3.4) элементы матрицы S – 1/li – ограничены сверху, т. е. параметры li ограничены снизу.
Для получения эффективных оценок параметров эконометрических моделей при нарушении условия (2.18), т. е. когда Cov(a)¹se2(X¢X)–1, в общем случае может быть использован обобщенный метод наименьших квадратов, разработанный А. Эйткеном.
Математическое обоснование ОМНК базируется на свойстве положительно определенной* ковариационной матрицы W, допускающей представление в виде произведения двух матриц:
W=p×p¢, (3.8)
где матрица p — невырожденная.
Из (3.8) непосредственно вытекает, что
p–1W×(p¢)–1=Е, (3.9)
и
(p¢)–1p–1=W–1. (3.10)
Для доказательства равенства (3.9) достаточно левую и правую часть выражения (3.8) умножить слева на p–1 и справа на (p¢)–1.
Равенство (3.10) непосредственно вытекает из свойств обращения произведения матриц.
Предположим, что матрица p известна. Умножим матрично-векторное уравнение исходной эконометрической модели у=Хa+e слева на матрицу p–1 и получим
у*=Х*a+e*, (3.11)
где
у*=p–1у; Х*=p–1Х ; e*=p–1e . (3.12)
Покажем, что ковариационная матрица вектора e* равна Е. Для этого запишем:
Cov(e*)=M=M=p–1Wp–1¢=E. (3.13)
Из (3.13) непосредственно вытекает, что se2=1.
Применяя к модели (3.11) обычный метод наименьших квадратов, получим вектор оценки a из следующего выражения:
a=(Х*¢Х*)–1Х*¢у*=(Х¢W–1Х)–1Х¢W–1у. (3.14)
Несложно показать, что оценки коэффициентов a, полученные на основании выражения (3.14), обладают свойствами несмещенности при конечном Т в случае детерминированных, а также и состоятельностью и асимптотической несмещенностью при Т®¥ – в случае стохастических исходных данных. Доказательство этих свойств при условии независимости значений столбцов матрицы Х и e в первом случае и асимптотических свойствах этих переменных (см. выражение (2.38)) – во втором приведены в разделе 2.1.
В частности, вектор а является несмещенной оценкой ОМНК вектора a, если M=0. С учетом (3.12) это условие эквивалентно выражению M=0, которое выполняется при конечной матрице p–1 и исходном предположении МНК M=0 о независимости факторов и ошибки эконометрической модели.
Ковариационная матрица оценок параметров, полученных на основании (3.14), определяется следующим выражением:
Cov(a)=(Х*¢Х*)–1=(Х¢W–1Х)–1=se2(Х¢S –1Х)–1. (3.15)
Последний результат получен, принимая во внимание свойство ошибки e* (3.13) и представления матрицы W в виде se2×S (постоянный множитель se2 выносится за скобки). С учетом этого очевидного результата выражение (3.14) может быть также представлено в следующем виде:
a=(Х¢S–1Х)–1Х¢S-1у. (3.16)
Аналогично, как и в разделе 2.1 (см. выражения (2.39)–(2.41)), доказываются свойства асимптотической несмещенности и состоятельности оценок ОМНК. В частности, из выражения (3.15) вытекает, что эти свойства имеют место, если матрица plim 
является ограниченной положительно определенной матрицей. В этом случае из (3.15) следует, что
Cov(a)=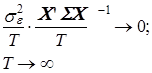 
В заключении данного раздела заметим, что матрица W, определенная выражением (3.4), для гетероскедастичной ошибки эконометрической модели, также является положительно определенной, а, следовательно, допускает представление (3.8). Из этого факта вытекает, что выражения (3.14) и (3.16) могут быть использованы для оценки коэффициентов этой модели и при гетероскедастичных ошибках с учетом замены ковариационной матрицы этих ошибок вида (3.1) на (3.4). Аналогичным образом и ковариационная матрица оценок параметров модели при ковариационной матрице ее ошибок, определенной выражением (3.4), находится из выражения (3.15).
Поможем написать любую работу на аналогичную тему