Метод инструментальных переменных

Для получения несмещенных (по крайней мере состоятельных) оценок параметров эконометрических моделей в ситуациях, когда имеют место (теоретически допускаются) корреляционные взаимосвязи между независимыми переменными xit и ошибкой et, теория  рекомендует подходы и методы, основанные на использовании инструментальных переменных.

Напомним, что в тех случаях, когда некоторые столбцы матрицы значений независимых переменных Х и вектор-столбец ошибки e  взаимосвязаны между собой, математическое ожидание второго слагаемого в правой части выражения (2.9) отлично от нуля, M¹0, и, следовательно, например, оценки МНК параметров модели, определяемые согласно известному выражению а=(Х¢Х)–1Х¢×у, оказываются смещенными, поскольку

M= M¹0.                      (3.51)

Заметим, что появление смещения у оценок МНК всех параметров моделей вызывает присутствие только одной независимой переменной, например, xi,   связанной с ошибкой e. В этом случае непосредственно видно, что произведение Х¢×e=(0,..., 0, сi, 0,...,0)¢, где константа   стоит на месте, соответствующем i-й  переменной, и, таким образом, имеем      (Х¢Х)–1¢×e=сi×(s0i,s1i,...,sni)¢= =сi×si, где sji   – j-й элемент i-го столбца si   матрицы (Х¢Х)–1. Из полученного результата вытекает, что в соответствии с выражением (2.9) имеем а=a+ сi×si. Из чего следует, что смещенными оказываются все оценки коэффициентов модели.

В эконометрике обычно исследуются асимптотические свойства оценок параметров моделей. В этом случае, если в пределе при Т®¥ существует зависимость между столбцами матрицы Х и ошибкой модели e, т. е.

то оценки МНК параметров эконометрической модели являются несостоятельными  (а, следовательно, и асимптотически смещенными).

 Это непосредственно вытекает из того факта, что второе слагаемое в правой части выражения

plim(a)=

отлично от нуля, поскольку из начальных условий (предположений) (2.42) вытекает, что

Использование инструментальных переменных теоретически позволяет устранить отрицательные последствия взаимосвязей независимых переменных и ошибки модели e, связанные с несостоятельностью оценок МНК параметров линейных эконометрических моделей.

Формально, без излишней строгости, выражение для вектора оценок МНК параметров эконометрической модели с использованием инструментальных переменных  может быть получено следующим образом.

Предположим, что существуют так называемые “инструментальные” переменные zi, число которых в общем случае совпадает с числом независимых факторов модели хi, i=1,2,..., n;  и при t=1,2,..., Т, каждая из которых характеризуется нулевыми корреляционными взаимосвязями с ошибкой эконометрической модели e. При заданном Т матрица значений инструментальных переменных Z имеет такой же размер, как матрица Х.

Умножим слева векторно-матричное уравнение на матрицу у=Х×a+e на матрицу Z¢. Получим

Z¢у=Z¢Х×a+Z¢×e,                                  (3.53)

С учетом того, что M=0, умножая выражение (3.53) слева на (Z¢Х)–1, непосредственно имеем

az =(Z¢Х)–1Z¢у,                             (3.54)

где az   – вектор оценок параметров эконометрической модели, полученный с использованием инструментальных переменных.

Результат (3.54) можно получить и традиционным путем. Для этого обозначим у*=Z¢у; Х*=Z¢Х; e*=Z¢×e. В этом случае выражение (3.53) имеет традиционный для эконометрической модели вид:

у*=Х*×a+e*.                              (3.55)

Используя для модели (3.55) традиционный для МНК критерий минимума суммы квадратов ошибки

s*2=(e*¢,e*)=(e¢Z×Z¢×e)=(Z¢у – Z¢Х×a)¢(Z¢у – Z¢Х×a)®min   (3.56)

и приравнивая вектор производных показателя s*2 по вектору параметров a  к нулю, , непосредственно получим следующее выражение для вектора оценок этих параметров:

az =(Х¢Z Z¢Х)–1 Х¢ZZ¢×у.                             (3.57)

Далее, принимая во внимание, что произведения матриц Х¢Z и Z¢Х равны между собой, т. е. Х¢Z=Z¢Х, выражение (3.57) несложно привести к виду (3.54).

az=(Х¢ZZ¢Х)–1Х¢ZZ¢×у=(Х¢Z)–1(Х¢Z)–1Х¢ZZ¢×у=(Х¢Z)–1Z¢×у=

=(Z¢Х)–1Z¢×у.

Покажем также, что при наличии у матрица Z размерностью Т´(п+1) в пределе при Т®¥ следующих свойств:

plim Z¢×e)=0;                               (3.58)

plim Z¢×Х)=åZ¢Х;                               (3.59)

plim Z¢× Z)=åZ¢Z,                               (3.60)

где матрицы åZХ и åZZ существуют и не вырождены, оценки параметров эконометрической модели, определенные выражением (3.54), являются состоятельными.

Для этого, как и при выводе выражения (2.9), подставим вместо вектора у в формулу (3.54) у=Х×a+e. Получим

az=a+(Z¢Х)–1Z¢e,                             (3.61)

В пределе при Т®¥ имеем

plimaz =a+plimZ¢Х)–1× plimZ¢e)=a+å–1Z¢Z×0=a.    (3.62)

Обратим внимание на некоторые свойства оценок параметров, полученных с использованием инструментальных переменных на основе выражения (3.54).

В частности, отметим, что в общем случае эти оценки являются неэффективными. В самом деле, вид ковариационной матрицы ошибки e*=Z¢×e  модели (3.53) свидетельствует о наличии в ее ряду автокорреляционных зависимостей даже в том случае, когда эти зависимости отсутствовали у ошибки e:

Cov(e*)=M=M= M=

=se2(Z¢Х)–1Z¢×Z(Z¢Х)–1,                       (3.64)

где дисперсия ошибки se2 на практике может быть оценена на основании следующего выражения:

В пределе при Т®¥ с учетом предположений (3.59) и (3.60) можно определить асимптотическую ковариационную матрицу оценок az  на основании следующего выражения:

asy.var(az)= plim=

=plim=

=plim(Z¢Х)–1)plim(Z¢e×e¢Z)plim(Х¢Z)–1=

=se2å–1Z¢ХåZ¢Zå–1Z¢Х.                          (3.66)

Для получения эффективных оценок на базе инструментальных переменных можно использовать обобщенных МНК. Для ковариационной матрицы ошибок модели, определенной выражением (3.63), оценки коэффициентов, полученные с использованием этого метода, определяются на основании следующего выражения, вытекающего из формулы (3.57):

az.0=(Х¢Z(Z¢Z)–1Z¢Х)–1Х¢Z(Z¢Z)–1×у=(Х¢Рz Х)–1Х¢Рz×у,      (3.67)

где Рz = Z(Z¢Z)––1.

Несложно показать, что ковариационная матрица оценок обобщенного МНК для инструментальных переменных имеет следующий вид:

Сov(az.0)=se2(Х¢Рz Х)–1,                         (3.68)

где на практике дисперсия ошибки se2 определяется следующим выражением:

Вектор оценок az.0, полученный на основании формулы (3.67) является асимптотически несмещенным. Это следует из выражения:

az.0=a+(Х¢Рz Х)–1(Х¢Рz ε),                         (3.70)

где

(Х¢Рz Х)=(Х¢Z)( Z¢Z) –1( Z¢X),

(Х¢Рz e)=(Х¢Z)( Z¢Z) –1( Z¢e).

Переходя в выражении (3.70) к пределу при Т®¥, с учетом свойств (3.58)–(3.60) получим

plimaz.0=a+(å Х ¢Zå–1Z¢ZåZ¢Х)–1åZ¢Хå–1Z¢Z×0=a.              (3.71)

Однако заметим, что на практике обобщенный МНК для оценки параметров моделей с инструментальными переменными применяется не часто. Это связано с тем, что дисперсии оценок их параметров, полученных на основе выражения ( .41), при удачном подборе инструментальных переменных увеличиваются не столь значительно, и такую потерю эффективности во внимание можно не принимать.

В самом деле, если инструментальные переменные zi   характеризуются достаточно сильной корреляционной связью (коэффициент парной корреляции rz,x®1) с соответствующими независимыми переменными хi, то при одинаковых масштабах этих переменных произведения матриц Z¢Z и Z¢X  будут приблизительно равными между собой и в этом случае, как это следует из выражения (3.64),

Cov(az)»se2(Z¢Х)–1»se2(Х¢Х)–1.                       (3.72)

И, наоборот, если переменные zi и хi  слабо взаимосвязаны между собой, то диагональные элементы матрицы (Z¢Х)–1  в силу того, что определитель ½Z¢Х½ уменьшается, существенно возрастают. В этом случае при использовании выражения (3.54) за несмещенность оценок приходится платить падением их эффективности. Этот вывод достаточно очевиден при рассмотрении однофакторной модели yt=a0+a1xt+et, при оценке параметров которой используется инструментальная переменная zt.

Несложно видеть, что оценка коэффициента a1 в этом случае согласно выражению (3.54) определяется по следующей формуле:

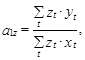
а выборочная дисперсия этой оценки по формуле:

где дисперсия se2 определена выражением типа (3.65) при п=1.

Из выражения (3.73) непосредственно видно, что при слабой зависимости между переменными хt  и zt   его знаменатель уменьшается (в пределе до нуля), и выборочная дисперсия параметра az   может стать как угодно большой.

Вследствие этого на практике инструментальные переменные zi  стремятся выбирать согласно следующему правилу: переменные zi   должны иметь сильные корреляционные связи с соответствующими переменными хi   и быть независимыми по отношению к ошибке модели e.

Выполнение этого правила в эконометрических исследованиях реальных процессов, для которых характерной чертой является корреляционная связь между независимыми факторами и ошибкой, достигается с помощью некоторых специальных приемов, правил формирования инструментальных переменных. Эти правила будут рассмотрены в соответствующих разделах данного учебника (см. главы V и VIII).

В заключении данного раздела рассмотрим некоторые особенности формирования матрицы инструментальных переменных Z. Очевидно, что общее число таких переменных должно быть равно количеству независимых факторов в модели. При этом, если какая-либо из переменных хi  оказывается не  связанной с ошибкой e, то она сама может выступать в качестве “инструментальной” переменной. В результате матрицу Х можно представить в следующем виде:

Х=,

где подматрица Х1 объясняет переменные, независимые по отношению к ошибке модели e, а подматрица Х2  – зависимые.

В этом случае матрица Z  имеет следующий вид:

Z=,

где Z2 подматрица инструментальных переменных, замещающих независимые факторы, образующие матрицу Х2.

Заметим также, что выражение Z(Z¢Z)–1Z¢Х=РzХ=, используемое в формуле (3.67), может рассматриваться как матрица расчетных значений факторов хit, полученных как оценки зависимых переменных при использовании в качестве независимых факторов инструментальных переменных zi, i=1,2,..., п. В самом деле, выражение (Z¢Z)–1Z¢хi определяет оценки коэффициентов следующей модели:

и, таким образом, (Z¢Z)–1Z¢Х=B, где B – матрица оценок коэффициентов моделей типа (3.74) для i=1,2,... п; имеющая следующий вид:

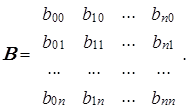
Тогда матрица Z¢B= представляет собой матрицу расчетных значений независимых факторов исходной модели, полученных в результате их выражения эконометрическими моделями типа (3.74) в зависимости от выбранных значений инструментальных переменных.

Отметим также, что если значения инструментальных переменных и независимых факторов исходной модели равны между собой, т. е. Z =X, тогда =Х(Х¢Х)–1 Х¢Х=Х.

С учетом этого равенства получим, что при частичной замене исходных факторов на инструментальные переменные матрица Z будет иметь следующий вид:

Z=,

где =Z(Z¢Z)–1 Z¢Х2 и Z=.

* Т. е. ошибка обладает нулевым математическим ожиданием M=0, ее дисперсия постоянна на всех участках рассматриваемого периода времени, а разновременные значения et   и et–j, j=1,2,…; независимы.

* В этом случае значения факторов будут обозначаться как  хi, t–1,  хi, t–2,...

** ( )¢ означает операцию транспонирования.

* Определение значений оценок параметров эконометрической модели осуществляется на основе исходной информации, выражаемой вектором у и матрицей Х, сформированных из наблюдаемых значений зависимой и независимых переменных.

* Вероятность р* в данном случае определяет границы области принятия гипотезы, р* – вероятность того, что при t<t*( k) гипотеза оказывается верной, т. е. 1– р*  – вероятность ошибки.

* Как было отмечено выше принятие решения о “целесообразности” удаления незначимого фактора основывается на анализе и ряда других критериев.

* Для некоторых классов эконометрических моделей (например, моделей временных рядов, моделей финансовой эконометрики) при выявлении соответствия модели и процесса основную роль играет также степень совпадения теоретических свойств модели со свойствами описываемого ею процесса (см. главы VI и VII).

* Следует, однако, отметить, что данные показатели корректно рассчитываются лишь в случае ошибки, в ряду которой отсутствуют автокорреляционные связи. Если же такие связи имеют место, то, вообще говоря, их расчетные значения, определяемые по приведенным ниже формулам, содержат ошибку, величина которой зависит от силы этой связи.

* В таком случае в качестве “меры точности аппроксимации” следовало бы использовать выражени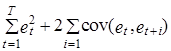е   , где  – значение ковариации ошибок et  и et+i .

* При этом увеличение объема выборки не должно нарушать ее однородность в том смысле, что закономерности рассматриваемых процессов являются теми же, как на “меньшей” выборке, так и на “большей”.

* Напомним, что асимптотическая несмещенность оценок является достаточным условием их состоятельности.

* Напомним, что первый выборочный коэффициент автокорреляции ошибки рассчитывается по следующей формуле:

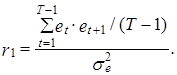
*G2=2=ET–2Х×(Х¢Х)–1×Х¢+Х×(Х¢Х)–1×Х¢Х×(Х¢Х)–1×Х¢=ET–Х×(Х¢Х)–1×Х¢=G.

* Это делается путем подстановки данного выражения в (2.99) и непосредственного перемножения матриц с учетом правила их транспонирования.

* Дисперсия переменной yt  в точке t может рассматривать как характеристика, построенная на множестве выборочных оценок математических ожиданий M  при соответствующих вариантах оценок их параметров, т.е. как

,

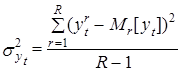где R – количество возможных вариантов оценок параметров и Mr= – выборочное математическое ожидание переменной yt  в r-м варианте. Аналогичным образом могут быть проинтерпретированы и определены и ковариации значений yt  и yt+j , t=1, 2,...Т; j= 1, 2,...,T–1

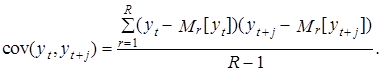
* Доказательство справедливости выражения (2.119) приведено в разделе 2.3.

** Состоятельность в данном случае характеризует определенное свойство функции правдоподобия, связанное с увеличением ряда наблюдений переменных модели при условии однородности выборки. Оно состоит в том, что с ростом Т максимальное значение этой функции (т. е. в точке оптимума) все более значительно превосходит ее значения в точках с другими неоптимальными значениями ее параметров.

* Напомним, что положительно определенная матрица невырождена, имеет положительный определитель и положительные главные миноры. Положительная определенность матрицы W  вытекает из ее симметричности.