Методы оценки дисперсии прогноза при детерминированном прогнозном фоне

Рассмотрим, не прибегая к излишней математической строгости, сначала общий подход к оценке дисперсии прогноза . Без ограничения общности предположим, что прогнозы  получены с использованием линейной эконометрической модели, ошибка которой характеризуется отсутствием автокорреляционных связей.

В соответствии с процедурой разработки эконометрического прогноза, рассматриваемое прогнозное значение зависимой переменной у, например, в момент времени Т+1, можно представить как случайную величину, определяемую по линейной модели типа (1.2) с учетом того факта, что ее параметры являются случайными величинами, а значения независимых факторов хi, T+1, i=1,2,..., n; – детерминированные величины:

где ai, i=0,1,..., n – коэффициенты эконометрической модели, рассматриваемые как случайные величины; eT+1  –  случайная ошибка модели в момент Т+1. Представим коэффициенты модели ai   в виде суммы их соответствующих оценок, являющихся математическими ожиданиями, и ошибок

где  математическое ожидание  аi  определено согласно используемому методу, например, МНК (см. выражение (2.8)), а характеристики ошибок Dаi  определены как элементы вектора Dа=(X¢X)-1X¢×e (см. выражение (2.9)).

Подставим выражение (12.9) в (12.8). В результате получим

где показатель

представляет собой математическое ожидание прогноза, а показатель

характеризует ошибку прогноза.

Ее дисперсия может быть определена согласно классическому выражению  в предположении о независимости ошибки модели eT+1 и ошибок коэффициентов модели Dаi, i=0,1,..., n; следующим образом:

где se2 – оценка дисперсии ошибки модели – дисперсия оценки аi,  а cov(аi, аj) – ковариация оценок параметров аi   и аj. Их значения определены как элементы ковариационной матрицы se2×(Х¢×Х)–1; х0,T+1 º1 (см. выражение (2.18)).

Еще раз отметим, что выражение (12.13) получено в предположении о независимости ошибки модели eT+1  в момент Т+1 и ошибок коэффициентов Dаi, которые согласно выражению (2.9) являются линейными функциями выборочных ошибок модели et, t=1, 2,..., Т.

Выражение (12.13) может быть представлено в матричной форме записи следующим образом:

где хT+1¢=(1, х1,T+1,..., хn,T+1) – вектор-строка детерминированных уровней прогнозного фона, представляющего собой набор значений независимых факторов в моменты Т+1.

Приведем также несколько более строгое доказательство выражения (12.14). Для этого запишем расчетное значение прогноза  в векторной форме:

Аналогично представим истинное значение прогноза уT+1

где a – вектор-столбец значений параметров модели; eT+1  – значение ошибки истинного прогноза.

С учетом представленных выражений ошибку прогноза согласно (12.6) выразим в следующем виде:

D уT+1=уT+1–=eT+1+хT+1¢×a–хT+1¢×a=

=eT+1+хT+1¢×a–хT+1¢×(X¢×X)–1× X¢×y.                       (12.17)

Подставляя в (12.17) вместо вектора наблюдаемых значений зависимой переменной y его выражение y=X×a+e, получим

D уТ+1=eT+1+хT+1¢×a–хT+1¢×(X¢×X)–1× X¢×(X×a+e)=

=eT+1+хT+1¢×a– хT+1¢×a– хT+1¢×(X¢×X)–1× X¢×e=

=eT+1– хT+1¢×(X¢×X)–1× X¢×e.                    (12.18)

С учетом (12.18) дисперсия ошибки прогноза  определяется следующим выражением:

s2()=M = M–2× хT+1¢×(X¢×X)–1× X¢×M+

+ хT+1¢×(X¢×X)–1× X¢×M×X×(X¢×X)–1×хT+1.             (12.19)

При справедливости предположений о независимости ошибки eT+1 и вектора ошибок модели e, гомоскедастичности и отсутствии автокорреляционных связей у вектора ошибки модели e имеем

M=0;

M=se2×E.

В этом случае с учетом того, что M=se2  легко показать, что выражение (12.19) преобразуется в выражение (12.14), с учетом замены se2 на se2.

Заметим, что выражение (12.19) определяет все случаи, отражающие возможные свойства ошибки эконометрической модели. В частности, когда у этой ошибки имеются автокорреляционные связи, например, первого порядка, т. е. et=r×et–1 +vt, vt ~N(0, sv2), Cov(v)=sv2×E  выражение (12.19) приобретает следующий вид:

s2()=se2–2×se2×хT+1¢×(X¢×X)–1×X¢×R+

+хT+1¢×(X¢×X)–1×X¢× Cov(e)×X×(X¢×X)–1×хT+1,         (12.20)

где вектор-столбец R=¢;

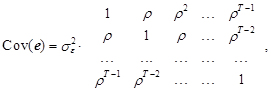
где r – коэффициент автокорреляции первого порядка.

Заметим также, что для такой модели математическое ожидание прогноза =M имеет следующий вид:

M= M= M= хT+1¢×a+r×eT. (12.21)

Выражая ошибку модели в момент Т eT   через ее оценку  еT

eT =еT – хT¢×а                                   (12.22)

и подставляя выражение (12.22) в (12.21), с учетом замены коэффициента r на его выборочное значение r и вектора a  на вектор a на практике получим

= r× yT+(хT+1¢– хT¢)×a.                 (12.23)

Несложно показать, что в этом случае расчетное значение прогноза в момент Т+k будет определяться следующим выражением:

=хT+k¢×a+ rk×eT.                       (12.24)

При наличии у ошибки модели только свойства гетероскедастичности выражение (12.19) приобретает следующий вид:

s2()=se2+хT+1¢×(X¢×X)–1× X¢×Cov(e)×X×(X¢×X)–1×хT+1,         (12.25)

где

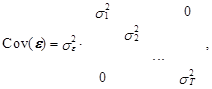
а st2  – дисперсия ошибки модели в момент t.