При случайном прогнозном фоне обычно предполагается, что значения независимых факторов в будущие моменты времени T+k являются случайными величинами, которые можно представить в виде суммы их математических ожиданий и случайных ошибок
При этом дисперсии и ковариации ошибок Dхi,T+1, Dхj,T+1, в общем случае предполагаются известными, и математические ожидания ошибок M=0; i, j=1,...,n; s2(х0)=M=0 в силу тождества х0º1.
Тогда, например, для момента Т+1 истинное значение прогноза определяется следующим выражением:
Далее обычно выдвигается вполне реалистическое предположение о независимости ошибок оценок параметров модели Dаi и соответствующего прогнозного фона Dхi,T+1. Их независимость, в частности, является следствием того, что параметры модели и прогнозный фон обычно определяются в ходе разных, не связанных между собой исследований.
После раскрытия скобок в выражении (12.27) несложно заметить, что расчетное прогнозное значение 
(математическое ожидание процесса) определяется выражением (12.11), а его ошибка DуT+1 – выражением следующего вида:
где х0, T+1º1, Dх0,T+1º0.
Дисперсия такой ошибки определяется на основании известного выражения s2(DуT+1)=M2 с учетом некоторых дополнительных предположений, касающихся свойств ошибки модели. В случае ее гомоскедастичности и отсутствия автокорреляционных связей, т. е. при se2=const, Сov(e)=se2×E, имеет место и независимость ошибок коэффициентов модели Dаi и ошибки eT+1. Независимость ошибки прогнозного фона и ошибки eT+1 практически очевидна.
В этом случае, возводя в квадрат правую часть выражения (12.28) и беря математическое ожидание от полученного выражения после несложных вычислений, получим
где cov(хi,T+1, хj,T+1) – ковариация случайных i-го и j-го значений прогнозного фона; при i=j, cov(ai, aj)=s2(ai,); cov(хi,T+1, хj,T+1)=s2(хi,T+1); cov(ai, aj)=cov(aj, ai) и cov(хi,T+1, хj,T+1)=cov(хj,T+1, хi,T+1); х0,T+1=0; s2(х0,T+1)=0; cov(хi0,T+1, хj,T+1)=0, j=1,...,n.
При выводе выражения (12.29) также учтено, что математические ожидания сомножителей типа Dаi×Dхi,T+1×Dхj,T+1×Daj, Dхi,T+1×Dаi×Daj×Dхj,T+1, Dаi×Dхj,T+1×Daj×Dхi,T+1 равны нулю в силу введенных предположений о равенстве нулю математических ожиданий рассматриваемых ошибок и независимости ошибок Dаi, Dхj,T+1, j=1,...,n.
Для получения выражения, определяющего дисперсию прогноза при случайном прогнозном фоне и свойствах ошибки модели, отличных от белого шума, представим выражение (12.28) в векторной форме записи:
D уT+1=хT+1¢×Da+DхT+1¢×a+D хT+1¢×Da+eT+1. (12.30)
Далее, как и в разделе 12.2, выразим векторы оценок коэффициентов модели и их ошибки в векторно-матричной форме записи a=(X¢×X)–1×X¢×y, Da=(X¢×X)–1×X¢×e, где e – вектор истинной ошибки модели, X – матрица наблюдаемых значений независимых факторов, y – вектор наблюдаемых значений зависимой переменной на интервале (1,Т). Получим
DуT+1=хT+1¢×(X¢×X)–1×X¢×e+DхT+1¢×(X¢×X)–1×X¢×y+
+DхT+1¢×(X¢×X)–1×X¢×e+eT+1. (12.31)
Дисперсию ошибки прогноза с учетом оговоренных выше предположений о независимости и свойствах ошибок Dаi, Dхj,T+1, i,j=0,..., n; определим как математическое ожидание от квадрата этой ошибки
s2()=M 2=хT+1¢×(X¢×X)–1× X¢×M×X×(X¢×X)–1×хT+1+
+у¢×X ×(X¢×X)–1×M ×(X¢×X)–1× X¢×y +M+
+M×X×(X¢×X)–1×DхT+1]+
+ хT+1¢×(X¢×X)–1× X¢×M. (12.32)
В предположении, что M=se2×E и независимости ошибок eT+1 и et, t=1,..., Т имеем
1) M×X×(X¢×X)–1×DхT+1]=
=se2× M= 
2) M=0.
В этом случае несложно показать, что выражение (12.32) приобретает следующий вид:
s2()=хT+1¢×Сov(a)×хT+1+a¢×Cov(Dх)×a+
M+se2, (12.33)
где Cov(Dх) – ковариационная матрица вектора ошибок прогнозного фона;
M= 
Несложно заметить, что выражения (12.29) и (12.33) эквивалентны.
При наличии у ошибки модели только свойства гетероскедастичности последнее слагаемое в правой части выражения (12.32) обращается в нуль, а ковариационная матрица ошибки имеет следующий вид:
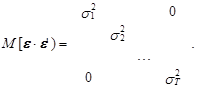
При наличии автокорреляционных связей у ошибки модели вектор M имеет специфический вид, определяемый характером этих связей.
Поможем написать любую работу на аналогичную тему