Линейная модель множественной регрессии имеет вид:
, (3.1)
где 
- расчётные значения исследуемой переменной, 
- факторные переменные. Каждый из коэффициентов уравнения 
имеет следующую экономическую интерпретацию: он показывает, насколько изменится значение исследуемого признака при изменении соответствующего фактора на 1 при неизменных прочих факторных переменных.
Фактическое значение исследуемой переменной тогда представимо в виде:
(3.2)
Для адекватности модели необходимо, чтобы случайная величина ε, являющаяся разностью между фактическими и расчётными значениями, имела нормальный закон распределения с математическим ожиданием равным нулю и постоянной дисперсией σ2.
Имея n наборов данных наблюдений, с использованием представления (2.2), мы можем записать n уравнений вида:
, (3.3)
где 
- значения исследуемой и факторных переменных в i-м наблюдении, а εi – отклонение фактического значения yi от расчётного значения yрi, которое может быть рассчитано с помощью (2.1) по значениям факторных переменных 
в i-м наблюдении.
Систему уравнений (2.3) удобно исследовать в матричном виде:
, (3.4)
где Yв – вектор выборочных данных наблюдений исследуемой переменной (n элементов), Xв – матрица выборочных данных наблюдений факторных переменных (
элементов), А – вектор параметров уравнения (m+1 элементов), а E – вектор случайных отклонений (n элементов):
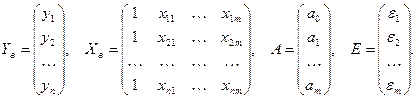(3.5)
Поможем написать любую работу на аналогичную тему