Косвенный метод оценки коэффициентов структурной формы систем взаимозависимых эконометрических моделей

В разделе 8.2. было показано, что использование МНК приводит к смещению оценок коэффициентов только структурной формы модели. В силу статистической независимости экзогенных переменных и ошибок структурной и приведенной форм оценки коэффициентов приведенной формы, полученные с использованием МНК, являются несмещенными (часто имеется в виду свойство их состоятельности). При этом ничто не мешает с помощью этого метода определить оценки коэффициентов каждого уравнения приведенной формы отдельно от других.

Это замечание наводит на мысль использовать для оценки коэффициентов структурной формы алгебраическое матричное уравнение (8.15) или его аналог, который может быть представлен в следующем виде:

С =–А–1 ×В ÞА×С +В =0,                               (8.36)

где 0 обозначает матрицу соответствующего размера с нулевыми элементами.

В выражении (8.36) в качестве неизвестных рассматриваются элементы матриц структурной формы А  и В, в то время как элементы матрицы приведенной формы С являются известными. Их можно определить путем использования МНК для оценки коэффициентов приведенной формы (8.13), (8.14) при известных значениях эндогенных и экзогенных переменных. Такой подход получил название косвенного метода оценки коэффициентов структурной формы системы взаимозависимых эконометрических моделей.

Теоретически косвенный метод представляется вполне приемлемым. Оценки коэффициентов матрицы С в силу независимости экзогенных переменных и ошибок соответствующих приведенных уравнений являются несмещенными и эффективными. Однако, к сожалению, как свидетельствуют результаты практических исследований, оценки коэффициентов структурной формы, полученные путем решения системы уравнений типа (8.36), свойство несмещенности, как правило, теряют. От оценок приведенной формы к оценкам структурной формы передается свойство состоятельности.  Кроме того, использование соотношений типа (8.36) для получения оценок коэффициентов структурной формы в общем случае вообще представляется неприемлемым. В самом деле, заметим, что система (8.36) содержит т´(n+1) уравнений (по числу элементов, содержащихся в матрице 0), а неизвестных коэффициентов в общем случае в ней т2+т×(n+1), в том числе т2  коэффициентов содержит матрица А, а т×(n+1) коэффициентов – матрица  В. Вследствие этого система (8.36) в общем случае не имеет единственного решения.

Вместе с тем часто в конкретных исследованиях (см. примеры раздела 8.2) на коэффициенты матрицы А и В накладывают дополнительные априорные ограничения, вытекающие, например, из теоретических предпосылок, эмпирических результатов, интуитивных предположений. При достаточном количестве таких ограничений число неизвестных параметров в матрицах А и В может быть снижено до уровня, обеспечивающего разрешимость системы (8.36).

В общем случае ограничения на структурные параметры моделей системы (8.36) подразделяются на исключающие и линейно однородные. При исключающих ограничениях коэффициент при отсутствующей в уравнении переменной приравнивается к нулю. При линейно однородных ограничениях значения некоторых коэффициентов приравниваются к конкретному числу, вытекающему из условий соотношений, в которые входят соответствующие им переменные. Так, в примере 8.3 в первых трех строках в матрице В использованы только исключающие ограничения. В четвертой строке матриц А и В использованы как исключающие, так и линейно однородные ограничения, соответствующие четвертому (балансовому) уравнению системы (8.34).

Рассмотрим условия, определяющие возможности использования выражения (8.36) для оценки коэффициентов структурной формы системы (8.11), более подробно для отдельного входящего в эту систему уравнения. Для этого представим выражение (8.36) с использованием матрицы D= в следующем виде:

                                                           С

×  Е п + 1     = D × G= 0,                          (8.37)

D= – матрица размера т´(т+n+1), образованная присоединением столбцов матрицы B к матрице A;

        С

G= Е п + 1      – матрица размера (т+n+1)´(n+1), образованная присоединением строк квадратной единичной матрицы Еп+1  размера (n+1) к матрице С;

G =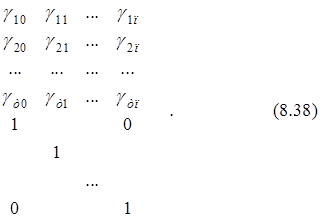     

Легко видеть, что выражение (8.37) является другим вариантом записи уравнения (8.36):

                            С

 D × G =  ×  Е п + 1     = A × С + B× Еп+1  = A × С + B = 0,

в котором матрица D образована неизвестными коэффициентами структурной формы, а матрица G – известными коэффициентами приведенной формы и единичными элементами матрицы Еп+1.

Рассмотрим произведение первой строки матрицы D на матрицу G, результатом которого является система однородных линейных уравнений, определяющая значения коэффициентов первой модели системы (8.11). Это произведение может быть представлено в следующем виде:

                                                         С

 d 1   ×  Е п + 1     = d 1× G = 0,                           (8.39)

где d1 – вектор-строка, составленная из коэффициентов первого уравнения системы (8.11), и 0 в правой части означает нулевой вектор-строку соответствующего размера.

В развернутом виде с учетом (8.9) и (8.14) систему (8.39) можно записать следующим образом:

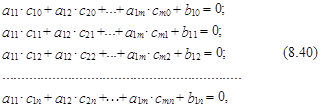
где aij – неизвестные оценки соответствующих коэффициентов матрицы А; b1j – неизвестные оценки коэффициентов первого столбца матрицы В; cij – известные оценки коэффициентов приведенной формы системы (элементов матрицы С); i=1,2,…,m; j=1,2,…,n.

Заметим, что система (8.40) выражает несколько другую запись уравнения (8.39), которая в векторно-матричной форме записывается как

                                                  С    ¢

 Е п + 1      × d 1 ¢  = 0¢.

Система (8.40) в общем случае включает в себя n+1 однородное уравнение и содержит т+n+1 неизвестное (оценки коэффициентов  a1i  и b1j, i=1, 2,..., m ; j=0, 1,..., n). Вместе с тем для однозначного определения этих оценок необходимо, чтобы количество неизвестных среди них было равно рангу матрицы G за вычетом единицы.

Если обозначить количество известных коэффициентов в строке d 1  как w1, а неизвестных – как w2, w1+w2=т+n+1, а ранг матрицы   G – как r(G), то это условие может быть представлено в следующем виде:

w2 =т+n+1–w1=r(G)–1.                             (8.41)

Выражение (8.41) известно как условие идентифицируемости системы (8.11) или ее некоторой модификации.

Напомним, что при выполнении условия (8.41) значения неизвестных коэффициентов системы (8.39) a1i  и b1j, i=1, 2,..., m; j=0, 1,..., n; определяются с точностью до множителя. Конкретные их значения можно получить, выбрав “подходящее” значение одного из коэффициентов заранее, а остальные в ходе решения системы (8.40) с использованием соответствующего метода (метода Гаусса, Крамера и т.п.). В нашем случае, как правило, единственное решение системы (8.39) можно получить, приравняв единице  коэффициент a11. Это естественное ограничение вытекает из формы записи первого уравнения системы (8.11) (см. примеры 8.1–8.3). Для других уравнений необходимо приравнивать к единице коэффициенты aii, i=2,..., m. При этом следует иметь в виду, что это естественное ограничение aii=1 не должно учитываться в соотношении (8.41), т. е. не должно входить в число w1 .

При относительно небольшом числе неизвестных параметров в первой строке матрицы D (эта относительность определяется соотношением w2<r(G)–1), система (8.39) становится переидентифицированной (сверхидентифируемой). Получение единственного решения в этом случае возможно, если, например, существуют ограничения на коэффициенты приведенной формы системы эконометрических моделей, уменьшающие ранг матрицы G. С этой же целью можно попытаться использовать приведенную форму с меньшим числом экзогенных переменных, если это не расходится с предпосылками, лежащими в основе системы моделей.

При условии w2>r(G)–1 система (8.39) является недоиндентифицируемой и без дополнительных ограничений на параметры структурной формы однозначно оценить их значения с помощью приведенной формы невозможно.

Заметим, что при решении системы (8.40) могут возникнуть определенные проблемы с учетом ограничений на параметры структурной формы. В основном это относится к линейно однородным ограничениям. В самом деле, если речь идет только об исключающих ограничениях, то их легко учесть, приравнивая к нулю соответствующие коэффициенты aik и bij. Для системы (8.40) это коэффициенты a1i  и b1j, i=1, 2,..., m; j= 0, 1,..., n; являющиеся элементами первой строки матрицы D.

Так, например, система (8.40) для первой модели из системы (8.30) с учетом исключающих ограничений на коэффициенты b17,..., b1,11  приобретает следующий вид:

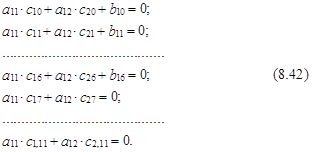
Однако, если для этой модели имели бы место какие-либо линейно однородные ограничения на параметры структурной формы типа b11=b12+b16, a12 +b11=0 и т. п., то для их учета при определении коэффициентов структурной формы требуется некоторая модификация систем (8.37), (8.39) и (8.42).

Рассмотрим альтернативный путь решения задачи оценки коэффициентов структурной формы системы взаимозависимых эконометрических моделей с учетом различного типа ограничений на ее параметры с использованием приведенной формы сначала для примера системы (8.30). Этот путь основан на модификации матрицы G путем ее  преобразования в матрицу G1 при сохранении для этой матрицы условия (8.37) (и соответственно (8.39)). Для этого заметим, что, например, исключающее ограничение на параметр b17 первого уравнения системы (8.30) может быть представлено в следующем виде:

d 1   ×      =0,                                         (8.43)

где 1 стоит на месте, обеспечивающем в результате умножения вектора d 1    на вектор ограничений выполнение условия b17=0.

Обозначим вектор-столбец в выражении (8.43) как g7¢. Число его компонент равно числу элементов вектора d1. Аналогичный вектор для переменной b18  обозначим как g8¢(он содержит единицу на месте, соответствующем элементу b18), для переменной b19 – g8¢,...

Расширим матрицу G  модели (8.30) за счет присоединения к ней векторов, отражающих исключающие ограничения, g7 ¢ , g8¢,..., g11¢. В результате получим матрицу G1 следующего вида:

G1 = = 

где единицы в присоединенной части стоят на местах, обеспечивающих в результате произведения вектора d1  на векторы g7¢,..., g11¢ выполнение условий b17=0, b18=0,..., b1,11=0.

В силу условия (8.43), выполняемого для исключающих ограничений на параметры b17,..., b1,11, для элементов матрицы G1 имеет место такое же соотношение, как (8.39) для матрицы G:

d 1   × G1 = 0.                                (8.45)

Однако заметим, что при этом, во-первых, матрица G1 расширена  по сравнению с матрицей G на 5 столбцов (по числу введенных ограничений) и ее ранг соответственно увеличился, и, во-вторых, вектор-строка d 1  записывается без исключающих ограничений. Ее элементы представляются в общей, а не в количественной форме записи.

Заметим, что на коэффициенты первой модели системы (8.30) могли быть наложены и ограничения других видов. Рассмотрим особенности их формализованного представления в матрице G1. Так, для линейного однородного ограничения b11=b12+b16  соответствующий ему вектор представляется в следующем виде:

g12¢=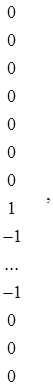  

где значения +1 и –1 стоят на местах соответствующих коэффициентов.

С участием вектора d1  это ограничение также записывается в виде произведения векторов d1×g12¢=0. Для его учета при оценке коэффициентов структурной формы необходимо расширить матрицу G также на вектор g12¢.

Некоторые сложности вызывает векторное представление неоднородных ограничений, содержащих в правой части вместо нуля значимое число. Примером такого ограничения является a12+b11=3. Однородный вариант записи этого ограничения предполагает использование коэффициента a11, который для получения решения затем нормализуется, т. е. выбирается равным 1(a11=1). В этом случае отмеченное ограничение приобретает вид a12+b11–3a11=0, и в векторной форме записи оно представляется следующим образом:

g13¢=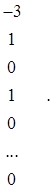   

Заметим, что векторы-ограничения достаточно просто формируются только для линейных ограничений на параметры. В случае нелинейных ограничений задача их учета при получении оценок параметров значительно осложняется. Для ее решения требуются специальные методы.

Таким образом, в случае линейных ограничений на параметры структурной формы модели в результате присоединения выражающих их векторов к матрице G  формируется матрица G1 размера (т+n+1)´(n+1+r), где r – количество учитываемых ограничений. Тогда по аналогии с условием существования однозначного решения системы (8.39) для матрицы G (см. выражение (8.41)), условие существования единственного решения системы (8.45) для матрицы G1 можно представить в следующем виде:

r(G1)=т+n ,                          (8.46)

т. е. ранг матрицы G1  должен быть на единицу меньше, чем число элементов в строке d1, где, напомним, т+n+1 – общее количество параметров модели структурной формы (количество элементов в соответствующей строке матрицы D), в нашем случае, в первой.

Из условия (8.46) непосредственно вытекает, что, если в матрице G отсутствуют линейно зависимые столбцы, то количество столбцов-ограничений, присоединенных к матрице G при формировании матрицы G1 , в случае единственного решения системы (8.45) должно удовлетворять равенству r=т–1. Иными словами, количество априорных ограничений должно быть равно числу взаимозависимых переменных в системе, уменьшенному на единицу.

При наличии в матрице G1 линейно зависимых столбцов в случае сверхидентифицируемости системы моделей количество вводимых ограничений должно превышать число т–1, r>т–1. Объединяя эти два результата в один, получим, что ненулевое решение системы (8.45) существует при выполнении условия

r ³т –1,                                    (8.47)

которое означает, что число априорных ограничений должно быть не меньше количества эндогенных переменных в системе взаимозависимых эконометрических моделей за вычетом единицы.

Рассмотрим вопросы идентифицируемости систем моделей на примерах 8.1-8.3. В примере 8.1 первое структурное уравнение системы (8.30) содержит в общем случае 9 неизвестных параметров (два при эндогенных переменных, включая у1, шесть при эндогенных и один свободный коэффициент). Всего система содержит одиннадцать экзогенных переменных (двенадцать параметров приведенной формы). Таким образом, матрица G, сформированная для этой системы имеет размерность 14´12 и ее ранг равен 12 (см. выражение (8.38)). Матрица G1  может быть образована присоединением к матрице G пяти исключающих ограничений на параметры b17,..., b1,11. Ее размерность будет равна 14´17.

Имея девять неизвестных параметров, системы уравнений (8.39) и (8.45), которые могут быть использованы для оценки коэффициентов структурной формы первого уравнения модели (8.30), являются сверхопределенными. Они содержат по четыре “лишних” уравнения, поскольку условие единственности решения системы (8.39) выполняется, если ранг матрицы G равен 8, а число присоединенных ограничений в матрице G1  равно 1.

В данном случае единственное решение этих систем может быть получено в результате наложения дополнительных ограничений на параметры приведенной формы модели (8.30). В частности, из пяти последних соотношений системы (8.42) вытекает, что такими ограничениями являются следующие равенства:

являющиеся следствием очевидного условия

Для примера 8.2 матрица G приведенной формы модели имеет следующий вид:

G =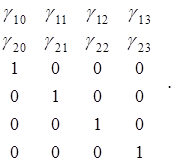    

Ее размерность равна 6´4, ранг матрицы равен 4.

Количество неизвестных параметров в первом уравнении структурной формы системы (8.32) равно 5. Имеется ограничение на коэффициент b13, b13=0. Таким образом, для первого уравнения системы (8.32) выполняются условия идентифицируемости, поскольку ранг матрицы G–r(G) равен 4. Аналогичный вывод следует из того, что число ограничений на его параметры равно количеству эндогенных переменных за вычетом единицы, 2–1=1. Значения параметров b10, a12, b11, b12 однозначно определяются из системы

d 1×G=0.

при условии a11=1.

Вместе с тем, второе уравнение системы (8.32) является сверхидентифицируемым. При определении значений его параметров следует учитывать ограничения на коэффициенты b21  и b22 (b21=b22=0). В этом случае на основании матрицы G  можно сформировать матрицу G2 (индекс 2 в данном случае обозначает номер модели-строки, для которой формируется соответствующая матрица ограничений). Матрица G2  имеет следующий вид:

G2  =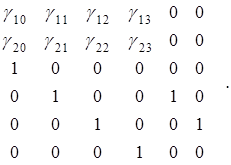   

Число учитываемых ограничений (дополнительных столбцов в матрице G2) превышает число эндогенных переменных на единицу. Следовательно, для идентифицируемости второго уравнения системы (8.32) необходимо вводить дополнительное ограничение на параметры структурной формы модели. Вид этих ограничений может быть получен исходя из анализа результатов произведения вектора d 2=(a21, a22, b20, 0, 0, b23) на матрицу С. Несложно заметить, что это произведение представляется в следующем виде:

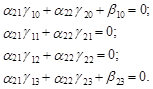
Из полученной системы непосредственно следует, что ограничения на параметры приведенной формы имеют вид, аналогичный (8.48)

Заметим также, что при решении системы d2×G =0 единственное решение при условии выполнимости указанных ограничений на параметры приведенной формы следует получать с учетом нормировки на коэффициент a22, приравнивая его к единице, т. е. a22 =1.

Для примера 8.3 матрица G приведенной формы модели имеет следующий вид:

G =    

Ее размерность составляет 10´6, ранг равен 6.

Количество неизвестных параметров в первой модели структурной формы системы (8.34) равно 4. Следовательно, эта модель является сверхидентифицируемой. Аналогично можно показать, что сверхидентифируемыми являются и другие две модели системы.

Четвертое уравнение системы (8.34) по своему содержанию является ограничением. Его необходимо учитывать при формировании матриц G1, G2 и G3  в случае ее использования при идентификации первых трех моделей. Данное ограничение записывается вектором-столбцом следующего вида:

   g =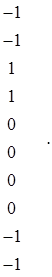   

Таким образом, например, для первого уравнения системы (8.34) матрица G1 примет следующий вид:

  G1 =G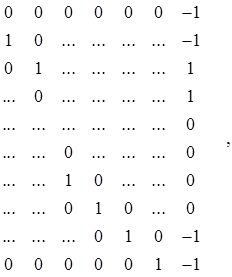     

где первый присоединенный столбец определяет ограничение a12=0, второй – a13=0, третий b12 =0,... , предпоследний – b15 =0 и последний – ограничение, выражаемое четвертым уравнением системы (8.34).

Рассмотренный в данном разделе материал свидетельствует, что оценки параметров структурной формы системы взаимозависимых эконометрических моделей с использованием приведенной формы этой системы могут быть однозначно определены только в случае идентифицируемости каждого из ее уравнений. При этом, поскольку оценки параметров приведенной формы являются несмещенными, то можно ожидать, что и оценки параметров структурной формы будут обладать этим свойством. На практике оценкам структурной формы передается свойство состоятельности. Вместе с тем, условие идентифицируемости каждой из моделей, входящих в систему, выполняется при наличии вполне определенного количества ограничений, накладываемых на ее параметры. Это следует из того факта, что в общем случае число уравнений, на основе которых определяются значения этих параметров, меньше их количества. При этом, заметим, что для идентифицируемости всей системы моделей необходимо, чтобы число ограничений в каждой из них было одно и то же. Естественно, что столь жесткие требования на количество ограничений на практике удовлетворяются далеко не часто. Вследствие этого рассмотренный косвенный метод при оценке параметров структурной формы системы взаимозависимых эконометрических моделей нельзя считать универсальным.

В следующем разделе будут рассмотрены более общие подходы к решению проблемы получения таких оценок, которые не имеют столь жестких ограничений по своему применению.