Модель и основная теорема факторного анализа.

В отличие от метода главных компонент факторный анализ заранее объясняет ковариационную (либо корреляционную) матрицу исходных переменных (признаков) наличием небольшого числа гипотетических факторов, присутствующих в исходных переменных. На языке корреляций это можно интерпретировать следующим образом. Вначале анализируется на значимость исходная корреляционная матрица, т.е. отличается ли корреляционная матрица значимо от единичной. Если это имеет место, то возникает вопрос: существует ли скрытая, иначе латентная, случайная величина  такая, что попарные корреляции между исходными переменными станут равными нулю, если влияние  уже учтено? Пусть после этого элементы корреляционной матрицы все еще отличны от нуля. Тогда пытаются найти две случайные величины  и  такие, что корреляции между исходными переменными станут нулевыми, если влияние  и  уже учтено, и так далее.

Тем самым корреляция между n наблюдаемыми признаками  связывается с тем фактом, что эти признаки зависят от меньшего числа других, непосредственно неизмеряемых переменных , которые принято называть общими факторами.

Модель факторного анализа   В общем случае нельзя гарантировать, что каждый из исходных признаков зависит лишь от m общих факторов, одних и тех же для всех признаков. Поэтому в факторном анализе постулируется, что наблюдаемый признак xi (i=1,2,…,n) зависит также и от некоторой характерной для себя остаточной (шумовой) случайной компоненты . Итак, линейная модель факторного анализа имеет вид:

,                  (11.1)

где коэффициенты  называют нагрузкой  j-го общего фактора на  i-й исходный признак, а матрицу , i=1,2,…, n; j=1,2,.., m –факторным отображением, либо матрицей факторных нагрузок.

Предпосылки факторного анализа.  Предполагают, что исходные признаки подчиняются многомерному нормальному распределению; общие факторы некоррелированы, а их дисперсии равны единице, следовательно, корреляционная матрица  общих факторов является единичной, т.е. ; характерные (остаточные) факторы    – нормально распределенные случайные величины, не зависимые друг от друга и от общих факторов. Это означает, что корреляционная матрица V  характерных факторов имеет диагональный вид. Все случайные величины имеют нулевое математическое ожидание.

Факторные нагрузки  и дисперсии  характерных факторов являются неизвестными параметрами, подлежащими оценке.

Вводя векторные обозначения:    ,

перепишем модель факторного анализа (11.1) в виде: .                                     (11.1а)

Ковариационная матрица  исходных признаков с учетом их центрированности по определению есть Cx = M,

где математическое ожидание берется по множеству реализаций вектора x.

Подставим в   выражение (11.1а):    Cx = M = M.

Раскрывая скобки в последнем выражении и учитывая, что общие и характерные факторы некоррелированы и, следовательно, M=0, M=0, а также неслучайный характер матрицы A, что позволяет выносить А за знак М, получаем Cx = AMA′+M.

M есть не что иное, как ковариационная матрица  общих факторов, а M ковариационная матрица V характерных факторов. Таким образом,    .                                        (11.2)

Согласно предпосылкам факторного анализа  есть единичная диагональная матрица. Следовательно,

.                                             (11.2а)

Соотношение (11.2) либо (11.2а) иногда называют фундаментальной теоремой факторного анализа. Она утверждает, что ковариационная матрица исходных признаков может быть воспроизведена с помощью матрицы факторных нагрузок и дисперсионной матрицы характерных факторов.

На практике обычно используют не ковариационную , а корреляционную матрицу  R исходных признаков. Переход от ковариационной к корреляционной матрице означает, что исходные центрированные переменные подвергаются нормированию делением значений каждого признака на среднее квадратическое отклонение этого признака. Такое преобразование позволяет избежать влияния масштаба измерения на результаты анализа. Преобразованные признаки будут иметь, очевидно, единичную дисперсию, их ковариационная матрица совпадает с корреляционной, а соотношение (11.2) примет вид: , (11.3)

где В и W имеют тот же смысл, что A и V, но для нормированных признаков.

Для диагональных элементов матрицы R выполняется соотношение: ,

где  – диагональные элементы матрицы W.

Сумму квадратов нагрузок общих факторов называют общностью: . (11.4)

Общность указывает ту долю единичной дисперсии исходного признака, которую можно приписать общим факторам. Часть единичной дисперсии, которая не связана с общими факторами, называют характерностью :    .                                      (11.5)

Характерность иногда разбивают на две составляющих, одна из которых, , называется специфичностью, а другая, , является дисперсией, обусловленной ошибкой, т.е. .

Факторное изображение допускает геометрическую интерпретацию. Согласно (11.1) точка в n-мерном пространстве исходных признаков представляется в виде линейной комбинации m+n координат точки в пространстве общих и характерных факторов, называемом также полным факторным пространством. Так как нагрузки общих факторов однозначно определяют дисперсии характерных факторов, то достаточно представлять признаки в m-мерном ортогональном пространстве общих факторов. Поскольку пространство общих факторов имеет размерность на n меньшую размерности полного факторного пространства, в факторном анализе используют обычно пространство общих факторов. Строки матрицы В факторных нагрузок рассматривают как точки в пространстве общих факторов. Координаты i-й точки есть . Соединяя эти точки с началом координат, получаем n векторов-признаков. Длина вектора, отвечающего i-му признаку, равняется, как видно из (11.4), корню квадратному из общности.

На рис. 13 в качестве примера приведена графическая иллюстрация факторного отображения.

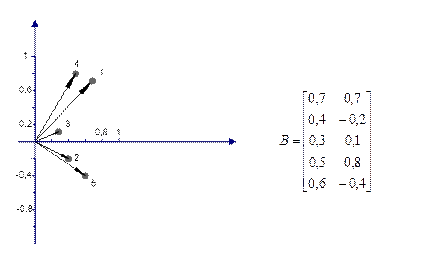
Рис.13. Графическая иллюстрация факторного отображения

Числа 1,2,…,5 около точек соответствуют номерам строк матрицы В, иначе номерам исходных признаков.