Основные этапы факторного анализа

Вычислительный аспект факторного анализа связан с определением факторного отображения В, дисперсий характерных факторов и оценкой значений общих факторов. Оценка этих параметров производится на основании экспериментальных данных, полученных в ходе наблюдений над N объектами (индивидами). Результаты наблюдений представляются в виде матрицы исходных данных, аналогичной (11.1). По матрице Х вычисляется корреляционная матрица R. Затем начинаются этапы собственно факторного анализа. Первый этап – оценка общностей. Если общности оценены, то по формуле (11.5) можно оценить характерности, а следовательно, и матрицу W, которая является диагональной согласно предпосылкам факторного анализа. Заменяя диагональные элементы матрицы R на оценки общностей, получают матрицу , которая является информационной основой второго этапа  выделения факторов. На этом этапе решают тем или иным способом матричное уравнение , получая в итоге ортогональную матрицу A. Возможно большое число матриц A, которые одинаково хорошо будут воспроизводить матрицу . Из них должна быть выбрана одна, что составляет содержание третьего этапа – вращения факторов. И, наконец, на последнем, четвертом, этапе оцениваются значения факторов для каждого объекта (индивида). На практике, однако, из-за большого объема вычислений часто ограничиваются первыми тремя этапами, причем первый и второй выполняются одновременно.

Выделение факторов. Выделение факторов предполагает установление числа и направления осей координат, соответствующих общим факторам, необходимым для отображения корреляции исходных переменных. С алгебраической точки зрения проблема факторов означает определение ранга матрицы А и оценивание ее элементов. Для решения задачи выделения факторов разработано достаточно много методов, однако основными в настоящее время следует признать два: метод главных факторов, наиболее широко употребляемый на практике, и метод максимального правдоподобия, имеющий прочный математико-статистический фундамент.

Метод главных факторов. Как следует из фундаментальной теоремы факторного анализа (11.3), . Приравняем вначале W нулевой матрице. Получим матричное уравнение .    (11.6)

Матричное уравнение (11.6) имеет множество решений: любое ортогональное преобразование Т, переводящее матрицу В в G, т.е. G = ВТ, удовлетворяет (11.6). Действительно, в силу ортогональности Т имеет место  и, значит, . Подставляя выражение для В в (11.6), получаем ,    поскольку T′T=I.

Как известно из линейной алгебры, ортогональное преобразование системы координат означает поворот системы как целого на некоторый угол вокруг начала координат. Выделяя некоторое предпочтительное направление и фиксируя тем самым угол поворота системы координат, можно обойти проблему неоднозначности решения системы (11.6).

Вернемся на время к методу главных компонент. Выбор осей координат здесь подчинен определенному требованию: каждая следующая ось ориентирована по направлению максимальной дисперсии в пространстве, ортогональном предыдущим главным компонентам. Матрица весовых коэффициентов А при этом составлена из собственных векторов ковариационной (корреляционной  R) матрицы. Следовательно,

,                                       (11.7)

где  – диагональная матрицa с элементами, равными собственным значениям корреляционной матрицы. Умножая (11.7) на  справа и учитывая ортогональность A , а значит , получаем:   .

Обозначим через  матрицу порядка , элементы которой равняются квадратному корню из соответствующих элементов матрицы Λ. Перейдем от  A к . Выражение для R примет вид:

.                                            (11.8)

Сравнивая (11.6) и (11.8), получаем, что в качестве оценки матрицы В можно взять матрицу  .

Таким образом, матрица факторных нагрузок получается из матрицы, составленной из собственных векторов корреляционной матрицы исходных признаков, с последующим умножением элементов собственного вектора, отвечающего i-му собственному значению  на .

Матрицы B и Q имеют разный порядок:    у В и    у Q, поэтому правильнее говорить, что оценкой будут первые  m столбцов матрицы Q.

Посчитав матрицу W равной нулю, мы для оценки матрицы B воспользовались моделью главных компонент. Строго говоря, под методом главных факторов понимают способ расчета, принятый в методе главных компонент, но примененный к матрице   (оценка общностей рассматривается ниже).

0ценка числа общих факторов. Общепризнанного метода определения числа m общих факторов, подлежащих выделению, не существует. Однако разработан ряд критериев, с помощью которых можно сделать достаточно обоснованное заключение.

Широкое применение получил сравнительно простой критерий собственных значений: выделять только те факторы, которые соответствуют собственным значениям, большим единицы.

Рассмотрим матрицу .Справедлива следующая цепочка равенств:     .

Полученное соотношение показывает, что сумма квадратов нагрузок i-го общего фактора на исходные признаки равняется i-му собственному значению . Но  характеризует вклад i-го общего фактора в полную дисперсию (напомним, что полная дисперсия равняется следу корреляционной матрицы R и ). Поэтому факторы, вклады которых меньше единицы, имеют долю дисперсии, меньшую единичной дисперсии исходных признаков, и их нецелесообразно включать в число общих факторов.

Считается также, что вклад общих факторов в суммарную общность должен составлять около 90%, а число общих факторов не должно превышать половины числа исходных признаков, т.е. m<n/2, а более точно, .

К проблеме оценки числа факторов можно подойти со статистической точки зрения. Ранее отмечалось, что если коэффициенты корреляции после учета m факторов незначимо отличаются от нуля, то нет необходимости вводить (m+1)-й фактор. Другими словами, равенство  должно выполняться в статистическом смысле (здесь  − матрица факторных нагрузок с числом факторов, равным m). Для оценки значимости матрицы R (в самом начале факторного анализа) либо матрицы  используется критерий Бартлетта − Уилкса 

с n(n-1)/2 степенями свободы, либо его аппроксимация   ,  где  – элементы матрицы .

Если все эти критерии дают не противоречащие друг другу решения, то удовлетворяются этими m факторами.

Метод максимального правдоподобия. В этом методе по выборочной корреляционной матрице  исходных признаков ищутся состоятельные и эффективные оценки неизвестных параметров − элементов матриц  В и W  для генеральной  совокупности. При построении функции максимального правдоподобия существенно используются предпосылки факторного анализа. Максимизация функции правдоподобия приводит к множественности результатов. Неоднозначность обходится требованием, чтобы матрица

                                        (11.9)

имела диагональный вид. Это условие соответствует требованию метода главных факторов о взаимной ортогональности факторов и их ориентации по направлению максимума дисперсии.

Система (11.9) может быть приведена к виду, удобному для вычислений итерационным путем:

.                           (11.10)

Скорость сходимости итерационной процедуры является весьма медленной и зависит от начального приближения B и W.

В методе максимального правдоподобия проблема определения числа факторов также существует. Пусть расчеты по (11.10) проведены для m общих факторов. Для проверки гипотезы о существовании m общих факторов можно воспользоваться критерием  

c  степенями свободы.

В этой формуле  – определитель матрицы корреляций, воспроизведенных с помощью m общих факторов. Если вычисленное значение критерия превышает табличное значение  при выбранном уровне значимости, то необходимо выделить факторов больше, чем m, по крайней мере , m+1.

Оценка общностей. Проблемы оценки общностей и оценки факторов тесно переплетаются. Если значения общностей установлены, то матрица  становится полностью известной и для нее может быть установлен ранг, т.е. минимально необходимое число общих факторов. Если вначале установлено число m общих факторов, то значения общностей подбирают таким образом, чтобы ранг матрицы  приближался к этому числу. Существует несколько способов оценивания общности. Мы их рассмотрим вкратце, поскольку при большом числе переменных точность оценивания общностей практически не сказывается на результатах факторного анализа.

Наиболее теоретически обоснован и чаще всего рекомендуется в качестве оценки общности i-го признака коэффициент множественной корреляции  i-го исходного признака с остальными (n–1) признаками.

Значение  вычисляется по формуле:   ,                                         (11.11)

где – диагональный элемент обратной корреляционной матрицы .

При проведении факторного анализа на ЭВМ во многих случаях используют итерационную процедуру вычисления общностей. На каждой итерации с помощью метода главных факторов определяют матрицу факторных нагрузок, а по ней находят оценки общностей, которые используются в следующей итерации. В качестве начaльного приближения используют коэффициент множественной корреляции (11.11).

Вращение факторов. Исследование с помощью факторного анализа следует признать успешным, если выявлено не только число общих факторов, но и дано содержательное толкование тем внутренним, скрытым причинам (общим факторам), которые обусловили результаты наблюдений. С целью облегчения процесса интерпретации общих факторов осуществляется третий этап факторного анализа – вращение факторов. Выше указывалось, что матричное уравнение  имеет бесконечное число решений (с точностью до ортогонального преобразования Т). Рассмотренные методы выделения факторов однозначно устанавливают положение системы координат, однако за счет введения дополнительных ограничений. Оси, соответствующие общим факторам, ориентируются последовательно по максимуму оставшейся дисперсии. Такая ориентация координат оказывается существенной в методе главных компонент, ориентированном на дисперсии. Основная цель факторного анализа – объяснение корреляций между исходными признаками. Окончательную ориентацию осей координат здесь производят из других соображений, а именно: с точки зрения содержательной интерпретации общих факторов. Для этого систему координат в пространстве общих факторов поворачивают как целое вокруг ее начальной точки, что эквивалентно умножению факторного отображения В на ортогональную матрицу Т справа.

Процедуру вращения рассмотрим на примере. По результатам успеваемости построена корреляционная матрица оценок по шести предметам: математике, физике, истории, литературе, родному языку, иностранному языку. Одним из методов выделены два общих фактора. Корреляционная матрица и матрица факторных нагрузок приведены в табл.26.

Таблица 26

Интерпретация полученных общих факторов представляет определенные трудности: необходимо выявить то общее, что обусловило высокие нагрузки на все шесть предметов у первого фактора, и на первый, второй и пятый – у второго, причем последняя значимая нагрузка − отрицательна.

На рис. 14 приводится графическая иллюстрация полученного факторного отображения (номера точек 1-6  соответствуют строкам матрицы факторного отображения).

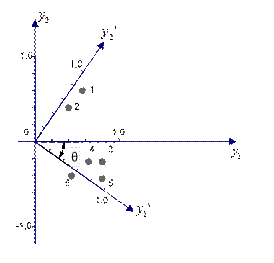
Рис.14. Поворот системы координат

Повернем оси координат по часовой стрелке так, чтобы сгусток, состоящий из точек 3-6, оказался как можно ближе к оси . Угол поворота  составляет как видно из рисунка, . Матрица преобразования T координат при повороте на угол  по часовой стрелке имеет вид:            .

Новые координаты точек Вн получаются перемножением матриц В и T , т.е.  .      (11.12)

Для рассматриваемого примера получим:  .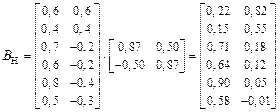

Интерпретация факторов, отвечающих матрице , несомненно проще: первый фактор существенно нагружает теперь только четыре исходных признака (история, литература, родной и иностранный языки), а второй  первые два признака (математика, физика), причем значимых отрицательных нагрузок нет. Естественно первый фактор назвать, например, гуманитарной одаренностью, а второй – склонностью к точным наукам.

Рассмотренный пример явился иллюстрацией геометрического подхода к проблеме вращения. Он предполагает визуализацию факторного отображения с последуюшим поворотом системы координат так, чтобы новые оси проходили через скопления точек. Если число общих факторов больше двух, то вращение осуществляется по шагам, учитывая каждый раз одновременно только две оси. Полная матрица преобразования состоит из произведения отдельных матриц преобразования для всех комбинаций пар факторов.

Только что рассмотренный пример на вращение показывает, что интерпретация общих факторов тем проще, чем «контрастнее» будут значения нагрузок – элементы столбца матрицы факторного отображения: либо близки к нулю, либо к единице. В этом случае каждый исходный признак получает наиболее простое описание на языке общих факторов (11.10) и, наоборот, при интерпретации каждого общего фактора учитывается минимальное число исходных признаков. Именно эти соображения легли в основу концепции простой структуры, широко используемой в факторном анализе. Термин «простая структура» служит для характеристики взаимосвязи между конфигурацией векторов, соответствующих исходным признакам, и осями координат пространства общих факторов. Если конфигурация векторов такова, что позволяет вращением координат достигнуть положения, при котором значительное большинство векторов-признаков окажутся на гиперплоскостях координат или вблизи них, то в этом случае говорят о простой структуре.

При многомерном факторном анализе в каждом столбце матрицы факторных нагрузок B найдутся несколько элементов, близких к нулю. Отсюда возникает вопрос: какое количество нулевых нагрузок достаточно, чтобы считать найденную гиперплоскость значимой? Решить этот вопрос можно с помощью критерия Баргмана. Для очередного i-го общего фактора подсчитывают число  признаков, для которых выполняется условие . Это число, называемое числом нулевых нагрузок, сравнивают с табличным qТ, соответствующим определенному числу исходных признаков. Если  при выбранном уровне значимости, то этот фактор считается определенным и его можно интерпретировать. Критерий Баргмана проверяет по сути дела гипотезу, что векторы, отвечающие исходным признакам, лежат друг к другу плотнее, чем можно было бы ожидать при случайном их расположении в пространстве общих факторов.

Кроме геометрического подхода к вращению факторов применяется аналитический подход. Применение этого подхода потребовало выработки критерия, с помощью которого можно было бы сравнивать результаты вращения.

Такой критерий опирается на концепцию простой структуры. В качестве меры простоты фактора выбирается дисперсия квадратов его нагрузок. Если эта дисперсия максимальна, то отдельные нагрузки близки к нулю или единице. Взяв сумму дисперсии по всем факторам и приводя векторы-признаки к единичной длине, получаем так называемый варимакс-критерий:   .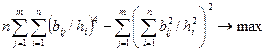

Процедура вращения осуществляется последовательно, учитывая каждый раз только две оси. Производится поворот на некоторый небольшой угол. Факторные нагрузки пересчитываются по формуле (11.12). Если при этом значение варимaкс-критерия возрастает, то эти оси вновь поворачиваются на тот же самый угол. Если же значение варимакс-критерия уменьшится, то переходят к другой паре координатных осей, и процедура повторяется.