Статистическое и чисто термодинамическое описание тепловых процессов различаются тем, что из законов статистической физики с неизбежностью вытекает существование флуктуаций. В то же время вероятность сколько-нибудь заметных флуктуаций в системе, содержащей большое число частиц, чрезвычайно мала.
Открытие многочисленных примеров флуктуационных процессов явилось блестящим подтверждением законов статистической физики и послужило одним из важнейших моментов в окончательном утверждении молекулярной теории.
В работах Эйнштейна и Смолуховского было показано, что целый ряд давно известных физических процессов обусловлен явлениями флуктуаций, и была развита комплексная теория этих вопросов, оказавшихся в прекрасном согласии с экспериментами.
Рассмотрим флуктуации в замкнутой системе.
Пусть система находится в состоянии статистического равновесия и имеет энтропию S0. Предположим теперь, что состояние системы изменяется так, что она переходит в неравновесное состояние с энтропией S.
Будем считать, что изменение состояния системы можно характеризовать изменением некоторого внутреннего параметра x, значение которого зависит от состояния всей системы.
В равновесии x=x0. Пример x – плотность ρ газа, находящегося в замкнутом теплоизолированном сосуде. В состоянии равновесия плотность постоянна по всему объему сосуда x0=ρ0=const.
В результате флуктуации система может самопроизвольно перейти в неравновесное состояние с переменной плотностью x= ρ(r).
Энтропия системы будет некоторой функцией параметра x:S=S(x). При этом в состоянии равновесия S0=S(x0) .
Вероятность застать систему в интервале значений x; x+dx должна быть пропорциональна статистическому весу (числу микросостояний) и величине интервала dx:
![]() .
.
Для изолированной системы верна формула Больцмана
![]()

Константа определяется из условия нормировки:
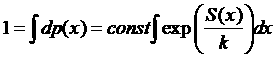
Или для функции распределения:
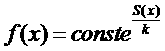 (*)
(*)
Прежде, чем приступить к интегрированию этой функции, надо ответить на вопрос о пределах ее применимости. Все распределения, приведенные выше, неявно подразумевают классичность поведения x. Поэтому надо найти условие, допускающее пренебрежение квантовыми эффектами.
Как известно из квантовой механики, между квантовыми неопределенностями энергии и какой-либо величины x имеет место соотношение
![]()
где dx/dt – классическая скорость изменения величины x.
Пусть τ – время, характеризующее скорость изменения нашей величины x, которая имеет неравновесное значение. Тогда 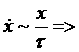
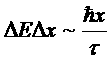
Ясно, что говорить об определенном значении величины x можно лишь при условии малости ее квантовой неопределенности ![]()
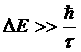
Таким образом, квантовая неопределенность энергии должно быть велика по сравнению с ![]() . Энтропия системы будет при этом иметь неопределенность
. Энтропия системы будет при этом иметь неопределенность
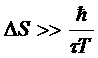
Для того, чтобы формула (*) имела реальный смысл, необходимо, очевидно, чтобы кавнтовая неточность энтропии была мала по сравнению сk:
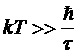 ;
; 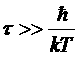
Это и есть искомое условие. При слишком низких температурах или при слишком быстром изменении x (слишком малом τ) флуктуации нельзя рассматривать термодинамически, т.к. на первый план выступают чисто квантовые флуктуации.
Выберем x так, что энтропия имеет максимум при x=x0=0. Поэтому
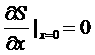 ,
, 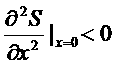
Величина x при флуктуациях очень мала. Разлагая S(x) в ряд по степеням x и ограничиваясь членом второго порядка, получим
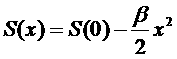
где β>0. Тогда получим распределение вероятностей в виде:
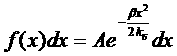
Нормирование константы A определяется условием
![]()
Хотя выражение для f(x) относится к малым x, но ввиду быстрого убывания подынтегральной функции с увеличением |x| область интегрированияможно распространить на все значения от -∞ до +∞. Произведя интегрирование, получим
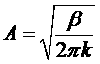 (интеграл Пуассона).
(интеграл Пуассона).
Таким образом, имеем для величины xраспределение:
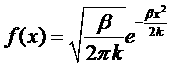 .
.
Эта формула называется распределение Гаусса. Если обозначить
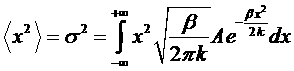 ,
,
то, беря интеграл, распределение можно записать в виде:
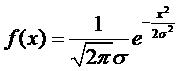 .
.
Функция f(x) имеет тем более острый максимум, чем меньше <x2>.
Отметим, что по известному <x2> можно найти аналогичную величину для любой функции j(x). Ввиду малости x имеем:
<(Dj)2>
= 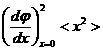
(подразумевается, что функция j(x) мало меняется при значениях x~<x2> и что производная dj/dx отлична от нуля при x = 0).
Если ![]() , то распределение Гаусса запишется в виде:
, то распределение Гаусса запишется в виде:
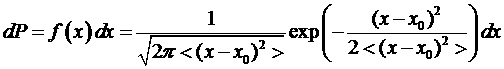 .
.
Поможем написать любую работу на аналогичную тему

