Процедура получения оценок максимального правдоподобия

Целевая функция типа (2.109) называется функцией максимального правдоподобия. Несложно заметить, что оптимальные значения оценок параметров a0*, a1*,..., an* и дисперсии фактической ошибки se2, соответствующие ее максимуму, должны обеспечивать и максимум ее логарифма. Иными словами, при определении значений этих оценок можно решать задачу максимизации  В таком случае в условиях независимости разновременных ошибок et  и et–i

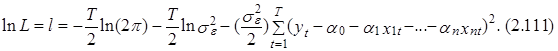
Не принимая во внимание первое постоянное слагаемое в правой части выражения (2.111), заметим, что оптимальные значения a0*, a1*,..., an*  и se2    в этом случае могут быть найдены путем решения следующей системы из п+2-х дифференциальных уравнений в частных производных по этим параметрам:

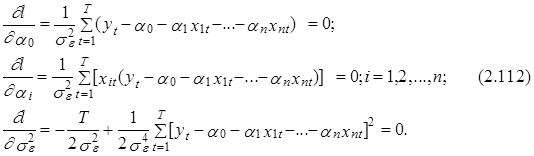
Для получения более компактной векторно-матричной формы записи решения системы (2.112) представим линейную эконометрическую модель  в векторно-матричной форме:

у=Х×a+e,                                    (2.113)

где вектор у  и матрица Х определены выражением (2.110) и вектор ошибки e  имеет такой же вид, как и вектор у; вектор параметров a=(a0, a1,..., an)¢.

На основании (2.113) вектор ошибки можно представить в следующем виде:

e=у –Х×a,                                     (2.114)

и последнее слагаемое в выражении (2.111) записать как скалярное произведение вектора ошибки строки на ее столбец. С учетом этого выражение (2.111) приобретает следующий вид:

(у–Х×a)¢×(у –Х×a).     (2.115)

Дифференцируя выражение (2.115) по неизвестному вектору параметров a и по неизвестной дисперсии ошибки se2, получим следующую векторно-матричную форму записи системы (2.112):

¶l/¶a = (– Х¢×у+ Х¢×Х×a)=0;

¶l/¶se2= 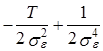 (у –Х×a)¢×(у –Х×a)=0.        (2.116)

Поскольку se2¹0, из первого уравнения системы (2.116) непосредственно получаем вектор оценок ММП коэффициентов линейной эконометрической модели в следующем виде:

a*=a=(Х¢Х )–1×Х¢×у,                            (2.117)

а из второго – оценку ММП дисперсии  ошибки эконометрической модели:

sе2 = (у –Х×a)¢×(у –Х×a)=

Заметим, что выражение (2.117)  ничем не отличается от своего аналога (2.8), полученного с использованием МНК, а  оценка дисперсии ошибки модели, полученная на основании выражения (2.118), является смещенной. Вследствие этого на практике используют несмещенную оценку дисперсии, определяемую следующим образом*:

Известно, что оценки параметров, полученные с использованием ММП, обладают свойством состоятельности** :

plim(a)=a,

plim(se2)=se2,

имеют асимптотически нормальное распределение и асимптотически эффективны,

                                        a                                 a                   a

                                                                             N              , I –1                            ,

                          se2                                              se2                        se2

где – символ асимптотического приближения, в данном случае закона распределения вектора-столбца оценок к закону нормального распределения с параметрами – их математическими ожиданиями  (a,se2)¢ и ковариационной матрицей I–1(a,se2)¢, обратной так называемой информационной матрице этих параметров.

Заметим, что состоятельность оценок ММП следует из совпадения с оценками МНК, которые, как было показано в разделе 2.1.2, являются состоятельными. Асимптотические свойства оценок ММП также определяются стремлением к нулю их дисперсий с ростом числа измерений, что следует из свойств элементов матрицы I–1(a,se2).

Напомним, что I (z) – информационная матрица случайного вектора z, определяется следующим образом:

I (z)= – M,                          (2.120)

где матрица  ¶2l/¶z¶z¢ имеет следующий вид:

¶2l/¶ z ¶ z¢ =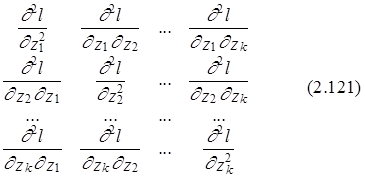  

и в нашем случае k=n+2 и z1=a0,..., zk– 1=an , zk  =se2.

Выполнив двойное дифференцирование выражения (2.116) по вектору a  и se2, получим

¶2l/¶a¶a¢=–Х¢Х/se2 ; –M=–Х¢Х/se2 ;

¶2l/¶a¶se2=–Х¢e/se4; –M=0.

Последнее равенство выполняется в силу предполагаемой независимости значений факторов хit (столбцов матрицы X) и ошибки e, являющейся “белым шумом”.

¶2l/(¶se2)2=T/2se4–e¢e/se6; –M=T/2se4, поскольку M=T×se2.

Таким образом, информационная матрица вектора (a, se2)¢ определяется следующим выражением:

I  

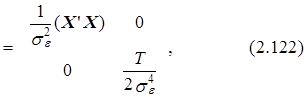
а ковариационная матрица этого вектора имеет следующий вид:

I–1  

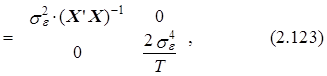
где (Х¢Х)–1   – представляет собой ковариационную матрицу вектора оценок параметров a, а  – дисперсию дисперсии модели se2.

Из выражения (2.123) вытекает, что ковариационная матрица вектора оценок параметров линейной эконометрической модели (1.2) имеет следующий вид:

Cov(a)=se2 ×(Х¢×Х)–1=Wa@se2 ×(Х¢×Х)–1.                 (2.124)

В выражении (2.124) учтено, что на практике оценка дисперсии истинной ошибки se2  может быть заменена ее оценкой se2, определенной согласно выражению (2.119) с использованием “фактических” значений ошибки et .

Из выражения (2.124) непосредственно следует, что дисперсии оценок параметров линейных эконометрических моделей , определенных по ММП, являются диагональными элементами матрицы  se2×(Х¢×Х)–1. Напомним, что среднеквадратические ошибки этих параметров () используются при определении значимости факторов модели (см. выражение (1.25)).

Таким образом, из результатов раздела 2.5 вытекает, что при предположении о нормальном законе распределения ошибки эконометрической модели и ее свойствах, определенных выражениями (2.20)–(2.24), оценки ее коэффициентов, полученные с использованием методов максимального правдоподобия и наименьших квадратов совпадают. Аналогичное совпадение отмечается и у ковариационных матриц этих оценок. Несложно показать, что в этих условиях у МНК и ММП совпадают также оценки параметров эконометрических моделей, полученные при ограничениях на их значения (см. выражение (2.91)).

Если же ошибки модели распределены по другому закону (например, Гаусса с тяжелыми хвостами, Стьюдента и т. п.), то вообще говоря, выражения для оценки коэффициентов, полученные на основе ММП, будут отличаться от их аналогов, полученных с использованием МНК.