Метод максимального правдоподобия

Из-за специфических свойств моделей с дискретными и ограниченными зависимыми переменными, метод максимального правдоподобия имеет некоторые особенности. Покажем их на примере моделей бинарного выбора.

Предположим, что наблюдения y1, y2,..., yT  независимы. Поскольку yt   может принимать только значения 0 и 1, то функция правдоподобия для бинарной модели имеет следующий вид:

a¢x t)] a¢x t).    (10.190)

Представим выражение (10.190) в несколько другой форме:

L=a¢x t)]a¢x t)]

где переменная yt  принимает значение 0 или 1.

Логарифм выражения (10.191) имеет следующий вид:

l=lnL=a¢x t)a¢x t)]}*.      (10.192)

Необходимыми условиями максимизации функции правдоподобия являются равенства нулю всех частных производных ее логарифма по параметрам a, т. е.

¶l/¶a=0.        (10.193)

где ft=f(a¢xt) и Ft=F(a¢xt), т. е. функции ft и Ft имеют аргумент a¢xt.

Подходы к решению системы (10.193), т. е. к получению оценок коэффициентов a, зависят от формы функционалов f(a¢x)  и F(a¢x). При этом заметим, что если F(a¢xt) нелинейны,  то уравнения в (10.193) также нелинейны. Для их решения (т. е. для получения оценок параметров a) используются итеративные методы, описанные в XI главе.

В частности, для logit-модели логарифм правдоподобия вылядит следующим образом:

а необходимыми условиями его максимизации являются:

¶l/¶a=0.                     (10.195)

Для нормального распределения логарифм  функции максимального правдоподобия может быть записан в следующем виде:

l=lnL=a¢x t)]+a¢x t).            (10.196)

В этом случае необходимые условия максимизации функции правдоподобия могут быть представлены в виде системы:

¶l/¶a=0,         (10.197)

где

jt =

Фt =ò

Рассмотрим особенности применения метода максимального правдоподобия для оценки двумерной probit-модели типа (10.72). Как было отмечено выше, вероятность того, что зависимые переменные Y1  и Y2 системы (10.72) для конкретного индивидуума принимают соответственно значения yt1 и yt2, рассчитывается как

P(Y1=yt1, Y2=yt2)=F2(wt1, wt2, pt*),              (10.200)

где

wtj= qtj×ztj ;   ztj=a¢jxtj,   j=1,2;                 (10.201)

rt*=qt1× qt2×r;                                (10.202)

qt1=2yt1–1; qt2=2yt2–1.                       (10.203)

Логарифм функции правдоподобия будет иметь следующий вид:

где

 F2(w1t, w2t, rt*)=ò ò          

а плотность этого распределения имеет следующий вид:

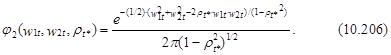
Первые производные логарифма правдоподобия по параметрам aj, j=1,2; и r  определяются как

¶lnL/¶aj=

¶lnL/¶r=

где

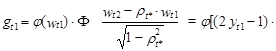a1¢xt1]´

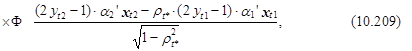
и индексы 1 и 2 в qt1  перевернуты для получения qt2.

Оценки максимального правдоподобия получаются путем одновременного приравнивания трех производных (по a1, a2  и r) нулю.

Модель Пуассона, являющаяся базовой моделью счетных данных (см. выражение (10.118)), представляет собой нелинейную регрессию. Логарифм функции правдоподобия для модели Пуассона имеет следующий вид:

l=lnL=+ yt×a¢×x t –ln(yt!)]=

+ yt×a¢×x t –ln(yt!)].              (10.210)

Необходимые условия его максимизации можно записать следующим образом:

¶ lnL/¶a=0.              (10.211)

Рассмотрим особенности выражений для оценки параметров усеченной регрессии (10.148).

В соответствии с выражением (10.139) плотность распределения усеченной случайной переменной уt  определяется как

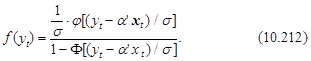
Логарифм функции правдоподобия является суммой логарифмов этих плотностей, т. е.

                   (10.213)

После некоторых преобразований выражения, на основании которых определяются оценки параметров модели примут следующий вид:

0;

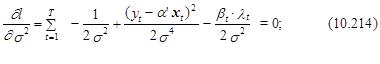
где bt =(b –a¢×xt)/s  и lt =j(bt)/.

Рассмотрим оценивание параметров tobit-модели (10.159). Логарифм функции правдоподобия для цензурированной регрессии может быть представлен следующим образом:

Первая часть выражения (10.215) соответствует классической регрессионной модели для нецензурированных наблюдений, а вторая часть – вероятностям для цензурированных наблюдений. Это – нестандартное выражение логарифма правдоподобия, так оно получено на основе сочетания дискретного и непрерывного условных распределений.

Необходимые условия максимизации функции правдоподобия будут иметь следующий вид:

0;

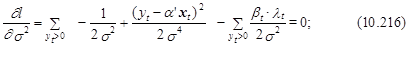
где bt =(b –a¢×xt)/s  и lt =j(bt)/.

Асимптотическая ковариационная матрица оценок* параметров моделей с дискретными и ограниченными зависимыми переменными, полученных с помощью метода  максимального правдоподобия, может быть определена двумя способами:

1) как обратная матрица к матрице математического ожидания вторых производных логарифма правдоподобия (взятой с противоположным знаком):

AsyCov(a)= (–M(¶2l/¶a¢¶a))–1,                   (10.208)

где AsyD(a) – асимптотическая ковариационная матрица оценок максимального правдоподобия.

Заметим, что матрица вторых производных логарифма правдоподобия используется в итеративных расчетах при получении оценок параметров.

2)  как оценка Берндта, Хола, Хола и Хаусмана (БХХХ-оценка):

где  для logit-модели и  для probit-модели (lt определено в выражении (10.193)).

БХХХ-оценка применяется при тестировании гипотез о коэффициентах моделей с дискретными и ограниченными зависимыми переменными.