Эконометрические модели с коррелирующими ошибками

Причины появления корреляционной зависимости между разновременными значениями ошибки эконометрической модели, вызывающие отличие вида их ковариационной матрицы от диагональной, могут быть разными. Часто невыполнение условия  Соv(e)=se2×Е, связывается  с не очень удачным выбором функционала модели f(a, x). Поясним сказанное на примере, представленном на  рис. 3.1.

Фактические данные, отражающие зависимость переменной у как линейной функции от переменной х на интервале (1, Х2), помечены “°“. На интервале (1, Х1) эти данные отражает линейная зависимость у=a01+a11x, а на интервале (Х1, Х2) – зависимость у=a02+a12x, где a01¹a02.  При этом ошибки на “своих” интервалах для данных моделей равны нулю. На обобщенном интервале (1, Х2) совокупность исходных данных аппроксимируются моделью у=a0+a1 x  с ошибкой на интервале (1, Х1) равной e1 и на интервале (Х1, Х2) – e2.  При этом, если интервалы равны, то e1=–e2. Несложно показать, что значения ошибки et  на интервале (1, Х2) связаны зависимостью et=ret–1, где  r ®1 с увеличением длины интервала (1, Х2).

              у                                  у= a02 + a12x

                                                                у= a0 + a1x

                                    у= a01 + a11x

                 0  1                 Х1                  Х2   x

Рис. 3.1. Иллюстрация причины возникновения корреляции

между ошибками эконометрической модели

Причиной появления ошибки явилось не вполне обоснованное предположение о том, что данные на интервалах (1, Х1) и (Х1, Х2) описываются одной и той же моделью.

Аналогично, автокорреляция в ряду ошибки может возникнуть, если для описания характера взаимодействия между переменными у и х вместо квадратической зависимости использовать линейную (рис. 2.1). В этом случае расчетные значения функции у=a0+a1x  на интервале (1, Х1) будут превышать фактические уровни переменной  у, а на интервале (Х1, Х2), наоборот, будет иметь место обратная ситуация, когда фактические значения зависимой переменой будут превосходить ее расчетные значения.

На практическом примере несложно убедиться, что коэффициент автокорреляции первого порядка для ошибки линейной модели в этом случае также будет значимым, т. е. ее ковариационная матрица – отличной от диагональной.

Часто появление зависимости между ошибками вызывается невключением в модель какой-либо объясняющей переменной, особенно если ее последовательные значения были зависимы между собой. В такой ситуации ошибка частично вберет в себя информацию – необъясненную изменчивость, обусловленную невключением в состав модели объясняющей переменной, в том числе и свойство зависимости последовательных ее значений.

Однако, как это было отмечено в разделе 3.1, даже если какие-либо подозрения относительно наличия автокорреляции между ошибками существуют априорно, то вид ковариационной матрицы ошибки и количественные характеристики ее элементов с более или менее приемлемой точностью априорно предсказать практически невозможно. Вследствие этого обобщенные МНК и ММП для оценки значений коэффициентов эконометрической модели в прямом виде не могут быть реализованы. В таком случае исследователи обычно применяют некоторые приемы, позволяющие получить более или менее удовлетворительную оценку ковариационной матрицы ошибки, ее некоторое приближение, которое можно было бы использовать в обобщенных методах оценивания. Некоторые из таких приемов будут рассмотрены в данном разделе на примере МНК.

Можно выделить два основных практических подхода к оценке недиагональной ковариационной матрицы ошибок эконометрической модели, отражающей существование корреляционной зависимости между ее значениями. Первый из них не требует использования предварительной информации относительно характера взаимосвязей между ее последовательными значениями et, et+1, et+2,... . Согласно этому подходу матрица Cov(e), рассматриваемая как оценка ковариационной матрицы истинной ошибки модели Cov(e),  находится эмпирически путем последовательного приближения по результатам этапов расчетов по построению промежуточных вариантов эконометрических моделей.

Первый этап полностью соответствует процедуре построения эконометрической модели, рассмотренной в главах 1 и 2. Согласно ему, на основании исходных данных – вектора у и матрицы Х – формируется уравнение эконометрической модели, затем с помощью МНК оцениваются ее коэффициенты, определяется вектор фактической ошибки е, значения которого проверяются, например, с помощью критерия Дарбина-Уотсона на наличие автокорреляции.

В том случае если факт корреляции установлен, то на основе эмпирического ряда ошибки е1, е2,..., еТ  оцениваются элементы ее ковариационной или корреляционной матрицы на основе следующих общих выражений:

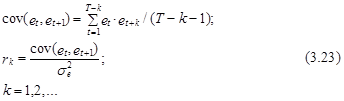
На практике обычно бывает достаточно оценить два-три  выборочных коэффициента корреляции, поскольку взаимосвязь между значениями ошибки с увеличением сдвига k резко ослабевает и значения коэффициентов r4, r5,... cтановятся практически не отличимыми от нуля.

На втором этапе определенную таким образом либо ковариационную матрицу фактической ошибки We, либо ее корреляционную матрицу Se  используют для оценки коэффициентов той же эконометрической модели с помощью обобщенного МНК (выражения (3.11), (3.13)). Далее вычисляется новый ряд фактической ошибки, происходит его проверка на наличие автокорреляции и, в случае подтверждения этой гипотезы, определяются новые матрицы We или Se. Затем с помощью обобщенного МНК строится третий вариант эконометрической модели и т. д.

Процедура построения модели завершается, если критерий Дарбина-Уотсона не подтверждает наличие автокорреляции в ряду фактической ошибки очередного варианта эконометрической модели. На практике для получения варианта модели с некоррелированной ошибкой часто достаточно провести одну итерацию. Вследствие этого такой подход получил название “двухшагового МНК”.

Подтверждением эффективности такого подхода является уменьшение дисперсий коэффициентов эконометрической модели каждого следующего варианта по сравнению с предыдущим, обычно наблюдаемое на практике. Напомним, что значения этих дисперсий рассчитываются как диагональные элементы матриц, определяемых выражениями (2.18) и (3.15).

Явление уменьшения дисперсий коэффициентов последовательных вариантов эконометрической модели может быть обнаружено на основе использования критерия Фишера для сумм элементов ковариационных матриц оценок коэффициентов модели двух последовательных ее вариантов. Дело в том, что сумма элементов матрицы Cov(a),  рассчитываемой согласно выражениям (2.18) для МНК и (3.15) для обобщенного МНК, выражает дисперсию суммы оценок коэффициентов модели. В этом случае, если выполняется условие

>F*(T–n–1, T–n–1, p*),                   (3.24)

где sm2 – сумма элементов ковариационной матрицы оценок Cov(a) на m-м шаге расчетов; F*(T–n–1, T– n–1, p*) – табличное значение критерия Фишера для числа степеней свободы n1=n2=T– n–1 и уровне доверительной вероятности p*, то гипотезу о том, что дисперсия суммы оценок коэффициентов модели уменьшилась на m-м шаге расчетов по сравнению с m–1, следует считать подтвержденной.

Заметим, что на практике вместо суммы элементов ковариационной матрицы оценок коэффициентов модели при определении их эффективности можно использовать фактическую дисперсию модели. Например, для МНК Cov(a)=se2×(Х¢Х)–1. Поскольку матрица Х¢Х постоянна, то отличия дисперсий коэффициентов полностью определяются значением se2.

При сопоставлении дисперсий оценок коэффициентов, полученных с помощью обобщенного МНК, подобную замену теоретически нельзя использовать, поскольку в формировании их ковариационной матрицы принимает участие корреляционная матрица ошибок (Cov(a)=se2×(Х¢S–1Х)–1). Однако, если допустить, что на m-м шаге расчетов значения коэффициентов корреляции изменились не слишком значительно по сравнению m–1-м шагом, то данной некорректностью можно пренебречь.

Другая группа подходов к построению эконометрических моделей с эффективными оценками коэффициентов при невыполнении условия Cov(e)=s2×Е основана на использовании априорной информации относительно возможного вида ковариационной матрицы ошибок. Эта информация может вытекать из анализа закономерностей измерения переменных модели, характера их взаимосвязей, формы самой модели и т. п.

Достаточно часто, предвидя появление ошибки спецификации модели (например, исходя из некоторого несоответствия ее уравнения эмпирическому графику входящих в нее переменных), исследователи заранее предполагают, что значения ошибки связаны между собой автокорреляционной зависимостью первого порядка

et =r1et–1+x t ,                                (3.25)

где r1 – коэффициент автокорреляции ошибки et  первого порядка; xt  – ошибка модели (3.25) с нулевым средним и конечной дисперсией sx2, которая неизвестна.

В отношении ошибки xt  обычно предполагают выполнение следующих свойств на интервале (1,Т):

– sx2= const;

– Cov(x) = sx2 Е;                                                                    (3.26)

Несложно показать, что при выполнении условия (3.25) ковариационная матрица ошибки эконометрической модели будет иметь следующий вид:

Cov(e) =W = se2 S = se 2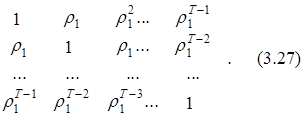   

Чтобы показать справедливость выражения (3.27), последовательно определим ковариации ряда et  с рядами e t–1, e t–2 и т. д.  Для сначала этого умножим левую и правую части выражения (3.25) на  et–1, полученный результат просуммируем  по t  и далее разделим на T–2. В итоге с учетом независимости переменных e t–1   и xt   получим

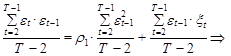
cov(e t , e t– 1)=r1se2.                                (3.28)

Проведем аналогичную операцию, умножив левую и правую части выражения (3.25) на e t–2. Получим

cov(et , e t–2)=r1 cov(et , e t–1)=r12se2                    (3.29)

и т. д.

                             cov(et , et–k )=r1kse2.

Таким образом, при выполнении условия (3.25) корреляционная матрица истинной ошибки эконометрической модели  оказывается определенной следующим выражением:

       S =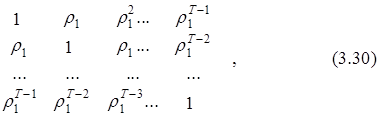 

в котором величина r1  однако остается неизвестной.

Вместе с тем, очевидно, что “хорошая” оценка r1 коэффициента корреляции r1 должна обеспечивать получение эффективных оценок коэффициентов эконометрической модели a0, a1,... an. Если предположить, что: а) как и ранее, эффективные оценки характеризуются минимальным значением суммы элементов ковариационной матрицы Cov(a); б) эта сумма (дисперсия) является непрерывной выпуклой функцией по r1, минимум которой соответствует “хорошей” оценке коэффициента r1, то теоретически эту оценку, как и эффективные оценки a0, a1,... an, можно определить с помощью несложной итеративной процедуры, в основе которой лежит обобщенный МНК. Ее суть состоит в следующем. Задается начальное значение r10 и на его основе (согласно выражению (3.27)) определяется Cov0(e). Далее с использованием обобщенного МНК (выражение (3.16)) определяются оценки a00, a10,... an0 и их ковариационная матрица  Cov0(a) (выражение (3.15)).

На втором шаге определяется значение r11=r10+Dr, где Dr – выбранный прирост оценки коэффициента автокорреляции, а затем повторяется последовательность расчетов первого шага.

Если r10 не являлось искомым оптимальным значением коэффициента автокорреляции, то при правильно выбранном знаке  Dr сумма элементов Cov1(a) будет меньше соответствующей характеристики матрицы Cov0(a).

Однако изложенная процедура практически не применяется. Причинами этого являются неизвестный характер зависимости суммы элементов ковариационной матрицы Cov(a)  от значений r1 (эта характеристика вообще может быть не слишком чувствительна к изменениям r1); неизбежные ошибки округления, которые приводят к смещению находимых оценок коэффициентов a00, a10,... an0; большой объем вычислений по каждому этапу процедуры. Все это делает ее трудно реализуемой даже на современных компьютерных системах.

В эконометрике обычно для получения эффективных оценок коэффициентов модели с коррелирующими остатками в предположении о справедливости зависимости (3.25) используются несколько другие подходы, предполагающие необходимость преобразования уравнения самой модели. Рассмотрим эти подходы более подробно.

Представим эконометрическую модель с учетом условия (3.25) в виде следующей системы уравнений:

                               уt =a0+a1x1t +...+an xnt+et ;

 et=r1et–1+x t.                                                      (3.31)

Поскольку et–1=уt–1–a0–a1x1,t–1–...–anxn,t–1, то систему (3.31) можно выразить единым уравнением

уt =r1уt–1+(1–r1)a0 +a1 x1t –r1a1x1,t–1+...+an xnt –r1an xn,t–1+xt . (3.32)

Критерием при определении неизвестных параметров выражения (3.31) является минимум суммы квадратов xt .

Обозначим произведения коэффициентов (1–r1)a0, r1a1,..., r1an  как b0, b1,... bn. Тогда  вместо выражения (3.32) можно записать

уt  =r1уt–1+b0 +a1 x1t –b1 x1,t– 1+...+an xnt –bn xn, t– 1+xt,        (3.33)

где b0 =(1–r1)a0, b1 =r1a1,..., bn =r1an .                                                      (3.34)

Из выражения (3.33) непосредственно вытекает, что, поскольку обычный МНК в общем случае не гарантирует выполнения условия (3.34), для оценки коэффициентов этой модели должен быть применен МНК, учитывающий эти нелинейные соотношения. МНК, учитывающий ограничения на параметры, да еще нелинейного вида, достаточно трудоемок с вычислительной точки зрения.

Вследствие этого на практике в таких ситуациях более широкое применение нашел так называемый двухшаговый метод наименьших квадратов, предложенный Дарбином (двухшаговый МНК Дарбина). Его суть состоит в следующем. На первом шаге, применяя обыкновенный МНК для оценки коэффициентов модели (3.33), определяют r1 – оценку коэффициента при уt–1. Далее формируются новые зависимая и независимые переменные ut=уt –r1уt–1; vit=xit –r1xi,t–1 , i=1,2,..., n;   t=1,2,..., T–1, зависимость между которыми выражается линейной эконометрической моделью следующего вида:

                      ut=b0+ a1v1t +...+anvnt +wt .                         (3.35)

где коэффициенты b0, a1,..., an  являются оценками соответствующих коэффициентов модели b0, a1,..., an, wt – фактическая ошибка модели.

Эти оценки определяются с помощью обычного МНК на втором шаге расчетов.

Метод Дарбина легко распространяется на ситуации, характеризующиеся наличием автокорреляционной зависимости между значениями ошибки более высокого порядка. Например, для автокорреляции второго порядка модель, связывающая текущие значения ошибки с двумя предыдущими, представляется в следующем виде:

et=g1et–1+g2et–2+x t.                                 (3.36)

где g1  и g2 – коэффициенты модели автокорреляции, отражающие характер зависимости текущего значения ошибки et от ее предшествующих значений et–1  и et–2. Оценки этих коэффициентов с1  и с2 определяются на основании значений выборочных  коэффициентов автокорреляции r1 и r2  – первого и второго порядка соответственно.

В этом случае по аналогии с выражением (3.32) можно записать

уt =с1уt–1+с2уt– 2+a1x1t+...+anxnt+(1–с1–с2)a0–с1a1x1,t–1–...–с1anxn,t–-1 – –с2a1x1,t–2 –...–с2anxn,t–2+wt.                         (3.37)

Применение двухшагового метода Дарбина к оценке коэффициентов модели (3.37) позволяет с помощью обыкновенного МНК на первом шаге определить оценки коэффициентов с1 и с2 при переменных уt–1 и уt–2 этой модели. Далее, как и в предыдущем случае, формируются   новые   переменные   ut=уt–с1уt–1–с2уt–2;   vit=xit–с1xi,t–1–с2xi,t–2, i=1,2,..., n;   t=1,2,..., T–1,  и на втором шаге оценки  коэффициентов исходной модели и a0, a1,... an  находятся опять же с помощью обыкновенного МНК, как и коэффициенты модели (3.35).

Отметим, что автокорреляционная зависимость ошибок с порядком более двух практически не встречается. В большинстве случаев порядок автокорреляции равен единице.

Заметим также, что корректность построенной модели в данном случае может быть определена на основе критерия Дарбина-Уотсона, рассчитываемого для остатков модели (3.35).