Тестирование изменчивости структуры эконометрической модели

Основная идея тестирования изменчивости коэффициентов эконометрической модели, имеющей систематический характер, состоит в проверке свойства случайности кумулятивной суммы ее ошибок при увеличении объема выборки (длины временного ряда) рассматриваемых переменных. В этом случае предполагается, что оценки коэффициентов линейной эконометрической модели, полученные по первым наблюдениям, в случае постоянства ее структуры, являются “достаточно хорошим” приближением для аналогичных оценок, полученных по следующим Т–k  наблюдениям, в том смысле, что прогнозные значения ошибок* , определенных на основании “предшествующих” оценок коэффициентов, по своим свойствам не отличаются от значений аналогичных ошибок ek+1, ek+2,..., eT,  определенных с использованием оценок коэффициентов, рассчитанных по всему объему выборки. Иными словами, если структура модели является постоянной, то прогнозные значения ошибок  также должны быть независимыми с нулевым математическим ожиданием (M=0, j=1,2,...) и конечной дисперсией.

В этом случае можно ожидать, что их накопленная сумма

окажется близкой к нулю, а сумма их квадратов (или их дисперсия, среднеквадратическое отклонение)

по своей величине не будут значительно отличаться от аналогичных показателей, рассчитанных по первым k наблюдениям.

В данной ситуации целесообразно рассматривать именно кумулятивную сумму прогнозных ошибок (сумму ее квадратов и т. д.), так как именно эти характеристики являются достаточно чувствительными к возможным изменениям коэффициентов модели, поскольку они обладают способностью накапливать систематическую составляющую ошибки, обусловленную этими изменениями.

Если даже с ростом объема выборки рассматриваемые свойства прогнозных ошибок не подтверждаются (их кумулятивная сумма, сумма квадратов и т. п. увеличиваются), то данный факт может служить свидетельством систематической изменчивости коэффициентов эконометрической модели.

На практике вместо самих прогнозных значений ошибки , t=k+1, k+2,..., T,  обычно рассматривают их стандартизованные значения wt, оцененные с использованием рекуррентной процедуры (4.1)–(4.14)* (см. раздел  4.1).

где, напоминаем, Ft–1=(X¢t–1×Xt–1)–1; Xt–1  – матрица первых t–1 значений независимых переменных размера (t–1)´(п+1); хt  – t-я строка значений независимых переменных в полной матрице X; at–1 – вектор оценок  п+1 коэффициентов эконометрической модели, определенных по наблюдениям t–1.

Таким образом, числитель в выражении (9.3) представляет собой прогноз ошибки модели в момент t, коэффициенты которой определены по предшествующим t–1 наблюдениям, т. е. прогноз ошибки на одно наблюдение вперед:

а знаменатель этого выражения представляет собой стандартизующий эту ошибку коэффициент.

Можно показать, что при постоянной структуре модели значения wt, t=k+1,..., T независимы и одинаково распределены по нормальному закону с нулевым средним и конечной дисперсией s2, N~(0, s2). В этом случае сумма их (r–n–1) значений, обозначаемая как Wr, определяемая следующим образом:

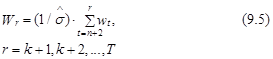
представляет собой сумму (r–n–1) независимых случайных величин, распределенных по стандартизованному нормальному закону N(0,1), где

– оценка дисперсии модели.

С учетом этого несложно показать, что wr  также распределено по нормальному закону со следующими характеристиками:

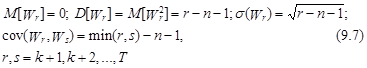
Напоминаем, что п+1 количество параметров модели.

С учетом (9.7) можно сформировать доверительные интервалы для последовательности случайных кумулятивных величин Wr. Поскольку каждая из них для r>п+1 имеет среднеквадратическое отклонение , то вся их совокупность в случае модели с постоянной структурой должна находиться в секторе, заключенном между кривыми и , где   – табличная константа, определяемая для стандартизованного нормального закона величиной доверительной вероятности p*. Напомним, что для p*=0,95, =1,96 (см. рис. 9.1).

               Wr

                              п+1     п+2    п+3                                         t

Рис.9.1. Доверительный интервал для кумулятивной суммы

стандартизованных ошибок модели

Таким образом, для любого r для эконометрической модели с постоянной структурой с п независимыми переменными имеет место следующее вероятностное условие, определяющее границы нахождения кумулятивной суммы Wr:

Выход значений Wr, r=k+1, k+2,..., Т за границы, определенные в выражении (9.8), является свидетельством того, что оценки коэффициентов эконометрической модели при увеличении количества исходной информации характеризуются систематическими изменениями.

Наряду с критерием кумулятивной суммы ошибок (прогнозных ошибок) для выявления факта систематической изменчивости коэффициентов модели может использоваться также критерий кумулятивной суммы квадратов ошибок. При этом последний критерий позволяет установить также и факт случайных изменений оценок параметров. Расчетное значение этого критерия представляет собой следующее отношение:

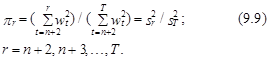
При этом можно показать, что величины sr2 и sT2 связаны следующим рекуррентным соотношением, которое можно использовать при расчете числителя отношения (9.9):

В самом деле, поскольку оценки коэффициентов модели, определенные по r–1 и r измерениям, удовлетворяют равенству:

то связь между соответствующими значениями sr–12  и sr2 может быть представлена в следующем виде:

Далее, выражая в последнем слагаемом правой части этого равенства матрицу Fr  через матрицу Fr–1 (см. выражение (4.5)):

после несложных преобразований с учетом (9.3) непосредственно получаем равенство (9.10).

Из (9.10) непосредственно вытекает, что значение показателя pr  из (9.9) определяется следующим соотношением:

0<pr £1.                                     (9.11)

При этом для моделей с постоянной структурой можно показать, что случайная величина pr   имеет бета-распределение со средним значением

и ее доверительный интервал при заданном уровне доверительной вероятности p* находится между прямыми, определяемыми уравнениями

где с0 – константа, зависящая от уровня доверительной вероятности p**.

Таким образом, нахождение показателя pr  при r=п+2, п+3,...,  Т–1  в границах, определенных выражением (9.13), является свидетельством постоянства структуры эконометрической модели. В противном случае можно утверждать, что оценки е параметров с ростом объема выборки меняются. При этом изменения могут иметь как систематический, так и случайный характер. Заметим здесь, что в отличие от нормированных ошибок wt, именно их квадраты (wt2) чувствительны к случайным изменениям оценок параметров.

При большом числе измерений Т (объеме выборки исходных данных) для проверки гипотезы о постоянстве структуры эконометрической модели можно использовать так называемый критерий гомогенности остатков, который является “мерой” равномерности распределения квадрата ошибки на отдельных участках рассматриваемого интервала времени (1,Т).

Значительный разброс этого показателя свидетельствует об изменчивости оценок коэффициентов модели.

Расчетное значение этого критерия формируется следующим образом. На интервале (1,Т) по имеющимся исходным данным строится эконометрическая модель и определяется сумма квадратов значений ее фактической ошибки s2(1,Т). Далее рассматриваемый интервал разбивается на  k частей (желательно равных для целей упрощения выкладок) (1, Т1), (Т1+1, Т2),...., (Тk–1, Т). На каждом из этих подинтервалов для построенной эконометрической модели рассчитывается соответствующая сумма квадратов ошибок sj2, j=1,..., k.

Известно, что значения s2(1,Т) и sj2, j=1,..., k связаны между собой согласно формуле представления общей дисперсии в виде суммы межгрупповой и внутригрупповой дисперсий. При этом отношение среднего квадрата отклонений между группами к среднему квадрату внутригрупповых отклонений в случае постоянства структуры эконометрической модели распределено по закону Фишера с (k–1)×(n+1) и степенями свободы.

Таким образом, для проверки гипотезы о постоянстве структуры модели на основе критерия гомогенности остатков необходимо рассчитать следующее дисперсионное отношение:

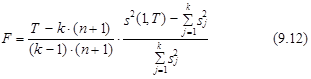
и сравнить его с табличным значением критерия Фишера   F*(n1, n2), выбранным по заданному уровню доверительной вероятности p* и числах степеней свободы n1=(k–1)×(n+1) и   n2=.

Гипотеза о постоянстве структуры эконометрической модели может быть принята с вероятностью p*, если будет выполнено следующее соотношение:

F< F*(n1, n2).

В противном случае структура модели может рассматриваться как переменная.

Несложно заметить, что критерий гомогенности остатков в большей степени подходит для выявления случайных изменений в оценках параметров эконометрической модели, поскольку его величина непосредственно не указывает на наличие каких-либо тенденций в изменениях ошибки на отдельных частях интервала (1, Т).

В некоторых случаях изменение структуры эконометрической модели может иметь вид скачкообразного переключения значений оценок ее параметров с одного режима на другой (скачкообразной смены значений оценок). Скачок в значениях оценок параметров обычно привязывается к какому-либо моменту  времени Т1, находящемуся на интервале (1,Т). Для статической совокупности исходных данных такой скачок может быть привязан к некоторому рубежному значению какой-либо из переменных (например, зависимой переменной уt).

В случае одного скачка эконометрическая модель, описывающая рассматриваемые процессы, как бы подразделяется на две модификации. Первая из них “работает” на интервале (1, Т1), а вторая – на интервале (Т1+1, Т). Таким образом, критерии скачка в данном случае должны достаточно четко указывать на наличие или отсутствие момента Т1, до которого целесообразно ( в случае его наличия) использовать первую модификацию модели:

а после него – ее вторую модификацию:

При этом обычно предполагается, что ошибки et(1) и et(2) распределены по нормальному закону с нулевым средним и дисперсиями s12 и s22 соответственно, et(1)~N(0, s12), et(2)~N(0, s22) и некоррелированы, Cov(e(i))=si2×E, i=1,2.

В случае необнаружения (отсутствия) такого момента критерий должен указывать на целесообразность использования единой эконометрической модели на всем рассматриваемом интервале (1,Т)

что эквивалентно равенству всех аналогичных коэффициентов в выражениях (9.15)–(9.17), ai(1)=ai(2), i=0,1,..., n, и равенству дисперсий s2=s12=s22.

При наличии нескольких скачков в параметрах эконометрической модели, например, в точках Т1, Т2,..., Тk  для описания рассматриваемых процессов необходимо использовать и соответствующее количество ее модификаций (по одной в каждой части интервала (1, Т)). Возможность построения модификации модели на каждой из частей интервала (1,Т) непосредственно указывает, что его продолжительность (объем выборки исходной информации) должна быть достаточно велика.

Рассмотрим основные идеи формирования критериев скачка в оценках параметров эконометрической модели, не привязываясь к конкретному моменту времени Т1. Предположим, что на интервале (1, Т1), где Т1  произвольный момент, была построена эконометрическая модель (9.15), т. е. были оценены ее коэффициенты и определены параметры распределения фактической ошибки et. Затем массив исходной информации был увеличен на t0 наблюдений. В связи с этим возникает вопрос: соответствует ли построенная модель вновь появившимся исходным данным или нет? В предельном случае t0=1, и тогда при отрицательном ответе на поставленный вопрос момент времени Т1+1 можно рассматривать как момент скачка ( переключения модели с одного режима на другой).

Для интервала (1,Т1) на основании МНК получим выражение вектора оценок коэффициентов модели (9.15) как многомерной случайной величины в следующем виде:

a1+e1=a1+u1,    (9.18)

где индекс (1) относится к значениям переменных, определенных на интервале (1, Т1) и u1=e1 –  вектор ошибки оценок параметров модели (9.15) a1.

Предположим, что на следующих t0 наблюдениях целесообразно использовать модель (9.16) с оценками, выражаемыми вектором a2 и ошибкой e2.

Определим ошибку прогнозов известных значений уt, t=Т1+1,..., Т1+t0, зафиксированных на втором интервале, полученных с использованием модели (9.15) первого интервала. Вектор этих ошибок может быть представлен в следующем виде:

a2 – X2×a1+e2 –X2×e1.    (9.20)

Вектор  состоит из t0 компонент и его математическое ожидание равно

X2×a2 – X2×a1 = X2×(a2 –a1).                (9.20)

В предположении о независимости ошибок e1  и e2  моделей (9.15) и (9.16) ковариационная матрица вектора  будет иметь следующий вид:

Cov()=Cov(e2)+ Cov=

=s22×E+ X2× Cov(e1) × X1×

=s22×E+ s12×X2 ×

Заметим, что в случае, когда дисперсии ошибок  s12 и s22  совпадают, выражение (9.21) имеет следующий вид:

Cov()=s2×(E+ X2 ×

В случае, когда t0=1, т. е. прогноз делается только на один шаг, матрица значений независимых факторов X2  трансформируется в вектор-строку, а ковариационная матрица Cov() преобразуется  в дисперсию прогнозного значения . Выражение для оценки этой дисперсии примет следующий вид:

D()=s2×=0, а конкретное значение , оцененное по левой части формулы (9.19), можно рассматривать как оценку случайной величины , дисперсия которой определена выражением (9.22). В этом случае отношение

распределено по закону Фишера со степенями свободы n1=1 и n2=Т1–п–1.

Таким образом, гипотезу о наличие скачка в оценках параметров эконометрической модели в точке Т1+1 следует отклонить с вероятностью p*, если F<F*(n1, n2). Вместе с тем, очевидно, что вывод о наличии скачка в оценках параметров модели по одному значению зависимой переменной и строке матрицы значений независимых факторов не является достоверным. Критерий (9.24) может скорее предупредить о возможности такого скачка в какой-либо точке, а его проявление должно быть подтверждено критериями, использующими информацию, соответствующую некоторой последовательности точек, образующих следующий  за Т1 временной интервал. Такие критерии можно разделить на две группы. Критерии первой группы не требуют построения следующей (очередной) модификации эконометрической модели на дополнительном временном интервале, критерии второй группы предполагают необходимость построения дополнительной модификации этой модели.

Критерии первой группы развивают изложенную выше идею формирования критерия скачка на случай нескольких точек, следующих за “рубежной” точкой Т1.  Рассмотрим основной подход к их формированию более подробно, но без использования громоздких выкладок.

Предположим, что за последней точкой Т1 интервала, на котором “работает” первая модификация эконометрической модели, определенная выражением (9.15) следует t0 точек. Согласно выражению (9.19) определим на каждой из них компоненты вектора w  как

На основании найденных значений wt  с использованием ковариационной матрицы Cov(w), определенной выражением (9.22), сформируем квадратическую форму следующего вида:

Cov-1(w)× w.                         (9.26)

В отсутствие скачка в оценках параметров эконометрической модели эта квадратическая форма будет распределена по центральному закону c2(t0) (вследствие свойства M=0), а в случае такого скачка –  по нецентральному c2(t0). Далее заметим, что в отношении выборочной дисперсии справедливо следующее соотношение  где s2 – выборочная дисперсия; s 2 – дисперсия генеральной совокупности; c2(n) – случайная величина, распределенная по закону Пирсона с числом степеней свободы n. Кроме того, отношение двух выборочных дисперсий из одной генеральной совокупности распределено по закону Фишера с n1 и n2 степенями свободы, т. е. F(n1,n2)=s12/ s22=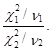 В этом случае, полагая, что первая выборочная дисперсия модели определена на основании значений wt  на интервале (Т1+1, t0), а вторая – на основании фактических значений ошибки модели на интервале (1, Т1), с учетом соотношения (9.22) можем записать:

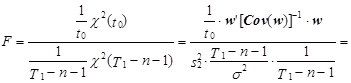
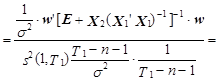
где  – сумма квадратов фактических значений ошибки модели на интервале (1, Т1); s 2 –  математическое ожидание дисперсии ошибки модели. Таким образом, отношение взвешенных сумм квадратов значений ошибки модели на интервале (Т1+1, t0) – прогнозной ошибки и на интервале (1, Т1) – фактической ошибки распределено по закону Фишера со степенями свободы n1=t0 и n2=Т1–п–1. Далее, как и в случае единственной дополнительной к интервалу (1, Т1) точке, гипотеза об отсутствии скачка в оценках параметров эконометрической модели на интервале (Т1+1, t0) принимается с вероятностью p*, если выполняется соотношение F<F*(n1, n2), где n1=t0,n2=Т1–п–1.

К критериям второй группы относится известный критерий Чоу. Согласно ему на интервалах (1, Т1), (Т1+1, t0) строятся первая и вторая модификации эконометрической модели, а на объединенном интервале (1, t0) – обобщающая (единая для двух интервалов) модель. Для каждого из вариантов модели определяются вектора ошибок e1, e2 и e – соответственно.

Расчетное значение критерия Чоу определяется по следующей формуле:

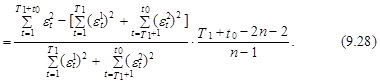
При этом значения критерия Чоу распределены по закону Фишера с п–1 и T1+t0–2n–2  степенями свободы. Поэтому гипотеза об отсутствии скачка в оценках параметров эконометрической модели в точке T1+1 принимается с вероятностью p*, если выполняется соотношение F<F*(п–1, T1+ t0–2n–2).

Если t0 недостаточно велико для оценки параметров второй модификации эконометрической модели на участке (T1+1, t0), то расчетное значение критерия Чоу определяется только с учетом ошибок первой модификации согласно следующему выражению:

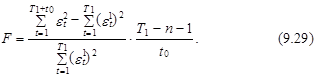
В данном случае значение F распределено по закону Фишера с t0 и T1–n–1 степенями свободы.

На практике обычно точка скачка T1+1 является неизвестной. Однако, сопоставляя графики процессов уt, хit, i=1,..., п; иногда удается приблизительно установить область ее нахождения на оси времени. В этом случае для определения точного местонахождения скачка рекомендуется определить расчетное значение используемого критерия в каждой точке этой области. Наилучшему решению соответствует максимальное значение критерия.

Для этих же целей может быть использован критерий логарифма отношений максимальных правдоподобий, рассчитываемый по следующей формуле:

где L(H0) – функция максимального правдоподобия, определенная на объединенном интервале (1, t0) для обобщенной эконометрической модели; L(H1) – функция максимального правдоподобия, определенная в предположении, что на интервале (1, T1) “работает” первая модификация этой модели, а на интервале (T1+1, t0) – вторая.

Можно показать, что на практике значение  рассчитывается согласно следующей формулы:

где s1 и s2  – среднеквадратические отклонения первой и второй модификаций эконометрической модели, а s  – обобщенной модели в целом.

Точке скачка оценок параметров эконометрической модели соответствует максимальное значение среди всех аналогичных значений, рассчитанных для рассматриваемой области его возможного местонахождения.